- 申 请 I D:SiJin233
- 个人邮箱:lhz1274590021@vip.qq.com
- 原创技术文章:
洛谷P4017 最大食物链计数 解决方案
题目重现
Delia给了你一个食物网,要你求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 1 秒的时间
由于这个结果可能过大,你只需要输出总数模上 80112002 的结果
输入:
第一行,两个正整数 n、m,表示生物种类 n 和 吃与被吃的关系数 m(n<=5000,m<=500000)
接下来 m 行,每行两个正整数,表示被吃的生物A 和 吃A的生物B
输出:
一行一个整数,为最大食物链数量模上 80112002 的结果。
样例:
输入样例#1
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
输出样例#1
5
解题思路
在开始分析之前,先复习一遍拓扑排序的知识,掌握拓扑排序才能理解并完成此题
我们不妨先根据测试样例画出一张图来方便分析

可以发现:食物网本质上是一张有向无环的AOV-网
食物网中的生物 —— 顶点
生物之间的关系 —— 有向边
最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者
根据题意得出,最左端的生产者入度为0,最右端的消费者出度为0
所以求 最大食物链的数量 可以转换为求 所有拓扑序列的数量 也就是求 入度为0 且 出度为0 路径的数量

再次分析能够发现,如蓝色箭头所示:
- 5 号点,出度为0,全部路径数量取决于:到 5 号点的三个点( 2 号、3 号、4 号)的食物链条数的总和
- 4 号点的全部路径数量取决于:到 4 号点的一个点( 3 号)的食物链条数
- 3 号点的全部路径数量取决于:到 3 号点的两个点( 1 号、2 号)的食物链条数的总和
- 2 号点的全部路径数量取决于:到 2 号点的一个点( 1 号)的食物链条数
- 1 号点,因入度为0,所以全部路径数量为1
得出结论:对于任一顶点的路径数量,都取决于和它连接的所有前一顶点的路径数量的总和
因此,我们得到了算法的核心思路:
在拓扑排序时,声明一个存放所有顶点路径数量的数组,在删除入度为0的顶点时,将 删除的顶点 的路径数量 加到 和它连接的所有后一顶点的路径数量上
最后,输出所有出度为 0 的顶点的路径数量总和 即为正确答案
代码模拟
为加深对 拓扑排序 及 本题核心思路 的理解,让我们来模拟一次操作测试数据的全部过程
- 第一步:初始化 顶点路径数量数组,将入度为0的 1 号点 加入队列
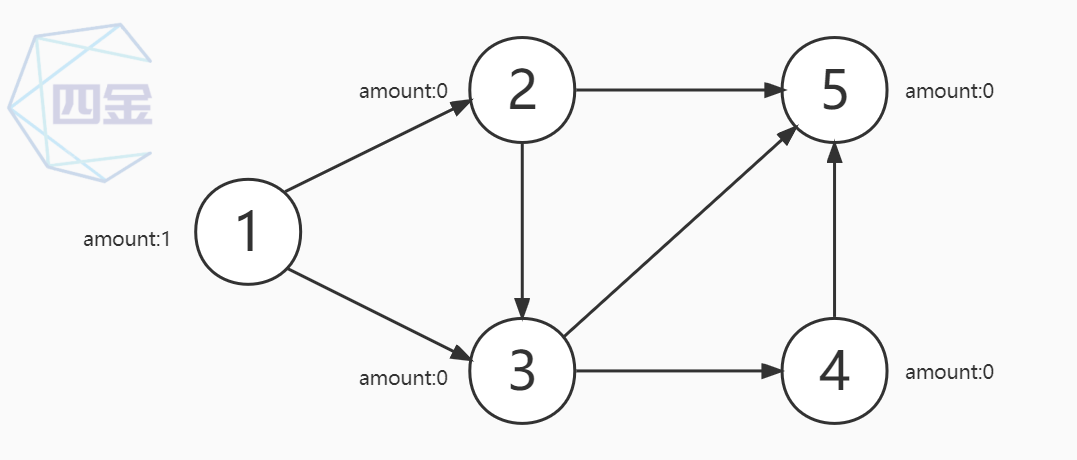
- 第二步:删除 1 号点,将 1 号点的路径数量 加到 和它连接的 2 号点和 3 号点的路径数量上,将入度为0的 2 号点 加入队列

- 第三步:删除 2 号点,将 2 号点的路径数量 加到 和它连接的 3 号点和 5 号点的路径数量上,将入度为0的 3 号点 加入队列
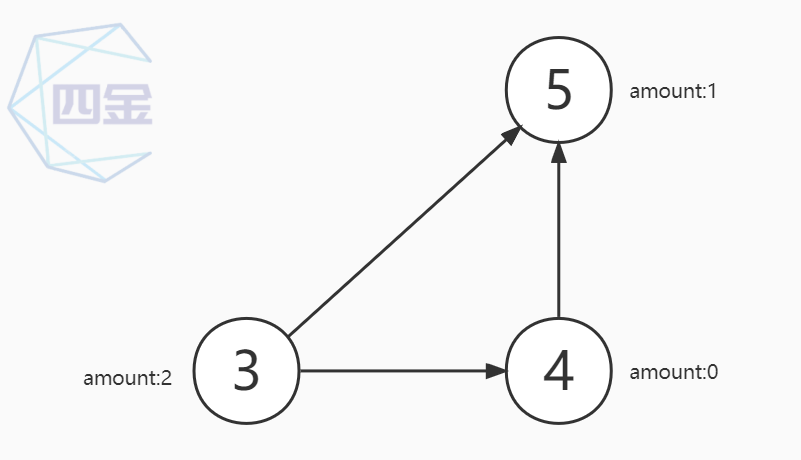
- 第四步:删除 3 号点,将 3 号点的路径数量 加到 和它连接的 4 号点和 5 号点的路径数量上,将入度为0的 4 号点 加入队列
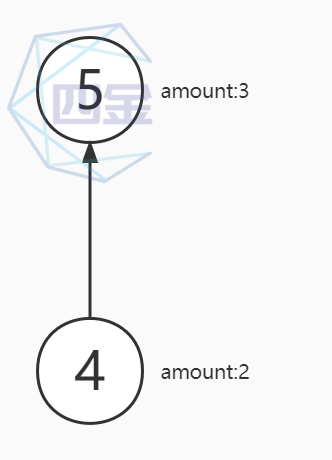
- 第五步:删除 4 号点,将 4 号点的路径数量 加到 和它连接的 5 号点的路径数量上,将入度为0的 5 号点 加入队列

- 第六步: 5 号点出度为0,且全部顶点遍历完成,输出最大食物链条数的数量 5
由此,我们可以在拓扑排序算法的基础上增加 记录路径数量 功能,从而写出全部代码
#include <iostream>
#include<queue>
using namespace std;
#define MOD 80112002
int n, m;//n:生物种类 m:吃与被吃的关系总数
int relation[5001][5001];//吃与被吃的关系
int in[5001], out[50001];//记录每个顶点的入度和出度
queue<int> Q;//拓扑排序队列
int amount[5001];//记录每个顶点的食物链条数
int i;
int result;//结果
void Process() {
//寻找入度为0的点进入队列
for (i = 1; i <= n; i++) {
if (in[i] == 0) {
Q.push(i);
amount[i] = 1;
}
}
//当队列不为空时持续处理
int cur;
while (!Q.empty()) {
cur = Q.front();
Q.pop();
for (i = 1; i <= n; i++) {
if (relation[cur][i] == 1) {
in[i]--;
amount[i] += amount[cur];
amount[i] %= MOD;
if (in[i] == 0) {
if (out[i] == 0) {
result += amount[i];//可能存在多个最右端出度为0的消费者
result %= MOD;
continue;
}
Q.push(i);
}
}
}
}
}
int main() {
cin >> n >> m;
int tempA, tempB;
//读入数据
for (i = 1; i <= m; i++) {
cin >> tempA >> tempB;
relation[tempA][tempB] = 1;
in[tempB]++;
out[tempA]++;
}
//处理数据
Process();
//输出结果
cout << result;
return 0;
}
 吾爱游客
发表于 2023-9-11 20:16
吾爱游客
发表于 2023-9-11 20:16
 发表于 2023-9-12 15:23
发表于 2023-9-12 15:23
 发表于 2023-9-12 18:52
发表于 2023-9-12 18:52