好友
阅读权限10
听众
最后登录1970-1-1
|
 Urkc
发表于 2024-3-5 12:50
Urkc
发表于 2024-3-5 12:50
复习内容a) 掌握原码、反码、移码和补码的表示及相互转换方法,它们的表示范围;(有符号数)b) 了解浮点数的表示格式,掌握 IEEE 754 单精度浮点数的格式和特点;(真值与单精度浮点数之间的转换)c) 掌握奇偶校验、海明校验的编码及解码过程。(校验码的生成)2.1数据表示的作用- 将数据按照某种方式组织,以便机器硬件能直接标识和使用
2.2数值数据的表示2.2.1数的机器码表示
- 将符号和数值一起编码表示的二进制
- 原码,反码,补码,移码
原码- 最高位表示符号位,符号位为”0“表示该数为正,符号位为”1“表示该数为负,数值部分与真值相同。
  例题1:求X=0的原码(假设机器数的数值部分长度是4位)定点整数:[+0]原=0,0000[-0]原=1,0000定点小数:[+0.0000]原=0.0000[-0.0000]原=1.0000例题2:用原码求(1-1)的真值(假设机器数的数值部分长度是4位)解:[1-1]原=[1+(-1)]原=[1]原+[(-1)]原=0,0001+1,0001=1,0010=[-2]真反码 例题1:求X=0的原码(假设机器数的数值部分长度是4位)定点整数:[+0]原=0,0000[-0]原=1,0000定点小数:[+0.0000]原=0.0000[-0.0000]原=1.0000例题2:用原码求(1-1)的真值(假设机器数的数值部分长度是4位)解:[1-1]原=[1+(-1)]原=[1]原+[(-1)]原=0,0001+1,0001=1,0010=[-2]真反码  例题1:求X=0的反码(假设机器数的数值部分长度是4位)定点整数:[+0]反=0,0000[-0]反=1,1111定点小数:[+0.0000]反=0.0000[-0.0000]反=1.1111例题2:用反码求(1-1)的真值(假设机器数的数值部分长度是4位)[1-1]反=[1+(-1)]反=[1]反+[(-1)]反=0,0001+1,1110=1,1111=[-0]真补码 例题1:求X=0的反码(假设机器数的数值部分长度是4位)定点整数:[+0]反=0,0000[-0]反=1,1111定点小数:[+0.0000]反=0.0000[-0.0000]反=1.1111例题2:用反码求(1-1)的真值(假设机器数的数值部分长度是4位)[1-1]反=[1+(-1)]反=[1]反+[(-1)]反=0,0001+1,1110=1,1111=[-0]真补码 - 负数加上”模“得到该负数的补数
- 正数和负数互为补数时,绝对值之和即为”模“
 如图所示,两个互为补码的数相加就回所有位数皆0,mod后的数2的次方数就是表示这个为几位计数器整数: 如图所示,两个互为补码的数相加就回所有位数皆0,mod后的数2的次方数就是表示这个为几位计数器整数: 例题:[+1101]真和[-1101]真的补码 例题:[+1101]真和[-1101]真的补码 小数: 小数: 例题:[+0.0110]真和[-0.0110]真的补码 例题:[+0.0110]真和[-0.0110]真的补码 例题2:求X=0的补码(假设机器数的数值部分长度是4位) 例题2:求X=0的补码(假设机器数的数值部分长度是4位) 例题2:用补码求(1-1)的真值(假设机器数的数值部分长度是4位)[1-1]补 =[1+(-1)]补 =[1]补+[(-1)]补 =0,0001+1,1111=[0,0000]补=[0]真原码转补码 例题2:用补码求(1-1)的真值(假设机器数的数值部分长度是4位)[1-1]补 =[1+(-1)]补 =[1]补+[(-1)]补 =0,0001+1,1111=[0,0000]补=[0]真原码转补码- 当X为正数时,[X]补=[X]原=X
- 当X为负数时,由[X]原转换为[X]补的方法:
- 反码法:[X]原除符号位外的各位取反加“1”
- 扫描法:自低位向高位,尾数的第一个“1”及其右部的“0”保持不变,符号位保持不变,左部的各位取反。
 移码 移码- 符号位中0表示负数,1表示正数
- 同一数值的移码和补码除符号位相反外,其他各位相同。
- 移码中的0表示也唯一;[+0.0000]移= [-0.0000]移= 1.0000
- 仅用于表示整数,通常表示浮点数的阶码
 补码与移码只差一个符号位4类机器码的应用 补码与移码只差一个符号位4类机器码的应用- 源码:用来表示浮点数的尾数
- 反码:已不用于表示数值数据
- 补码:50年代开始成为整数标准
- 移码:用于表示浮点数阶码
补码优势2.2.2定点数表示  - 若机器字长有n+1位,则:
- 原码定点小数表示范围为:-(1-2-n)~(1-2-n)
- 补码定点小数表示范围为:-1~(1-2-n)
- 定点小数主要用于表示浮点数的尾数
  - 若机器字长有n+1位,则:
- 原码定点整数的表示范围为:-(2n-1)~(2n-1)
- 补码定点整数的表示范围为:-2n ~(2n-1)
2.2.3浮点数表示浮点数表示  尾数为定点小数,可正可负,阶码为顶点整数,可正可负。 尾数为定点小数,可正可负,阶码为顶点整数,可正可负。 - es:阶码的符号位
- ms:位数的符号位,它是整个浮点数的符号位,反映了该浮点数的正负
- e:反映浮点数的表示范围,越大范围越大
- m:反映浮点数的精度,越大精度越高
浮点数的表示范围 浮点数的规格化 浮点数的规格化
- 尾数真值的最高数位为1 r=2[url=]image.png[/url]
- 原码——不论正数,负数,最高数位为1
- 补码——符号位和最高数位不同
 特例: 特例: 浮点数特点 浮点数特点
- 在移码中,最高位为“0”表示负数,最高位为“1”表示正数。
- 移码为全0时,它所对应的真值最小,为全1时,它所对应的真值最大。
- 真值0在移码中的表示形式是唯一的,即[+0]移=[-0]移=100…0。
- 移码把真值映射到一个正数域,所以可将移码视为无符号数,直接按无符号数规则比较大小。
- 同一数值的移码和补码除最高位相反外,其他各位相同。
- 简化机器中的判零电路。当阶码全为0,尾数也全为0时,表示机器零。
IEEE754标准浮点数 - 符号ms:判断正负
- 尾数:原码表示,规格化尾数最高位总是1,所以隐含表示,省1位 尾数精度=尾数的位数+1
- 阶码:移码表示 (12)10=(1100) 1.1×23
   例题2-7:将(20.59375)10转换成IEEE754单精度浮点数格式的十六进制机器码。(1)十进制数→二进制数 (20.59375)10=(10100.10011)2(2)非规格化数→规格化数 10100.10011=1. 010010011×24(3)可得:符号位S=0 阶码E=0111 1111+100=1000 0011 尾数M=0100 1001 1(4)单精度浮点数格式为 0; 1000 0011; 0100 1001 1000 0000 0000 0000表示为十六进制的代码:(41A4C000)16例题2-8:把单精度浮点数C1360000H转换成为十进制数(1)十六进制→二进制形式,并分离出符号位、阶码和尾数。 例题2-7:将(20.59375)10转换成IEEE754单精度浮点数格式的十六进制机器码。(1)十进制数→二进制数 (20.59375)10=(10100.10011)2(2)非规格化数→规格化数 10100.10011=1. 010010011×24(3)可得:符号位S=0 阶码E=0111 1111+100=1000 0011 尾数M=0100 1001 1(4)单精度浮点数格式为 0; 1000 0011; 0100 1001 1000 0000 0000 0000表示为十六进制的代码:(41A4C000)16例题2-8:把单精度浮点数C1360000H转换成为十进制数(1)十六进制→二进制形式,并分离出符号位、阶码和尾数。 (2)S=1,E=1000 0010;M=011011 e=E-127=1000 0010-0111 1111=00000011=(3)10 实际尾数为:1.M=1. 011011(3)得到N= (-1)s ×1.M× 2e=-(1. 011011) × 23 =-(1011.011)2=-(11.375)10理解 (2)S=1,E=1000 0010;M=011011 e=E-127=1000 0010-0111 1111=00000011=(3)10 实际尾数为:1.M=1. 011011(3)得到N= (-1)s ×1.M× 2e=-(1. 011011) × 23 =-(1011.011)2=-(11.375)10理解 e=4 e=E-127 E=131 阶码为8位M尾数=010010011 尾数为23位32位单精度浮点数编码格式 e=4 e=E-127 E=131 阶码为8位M尾数=010010011 尾数为23位32位单精度浮点数编码格式 2.1数据信息的校验2.4.1码距和校验 2.1数据信息的校验2.4.1码距和校验- 数据校验码:能够发现错误并且能够自动纠正错误的数据编码,又称之为“检错纠错编码”
 - 码距:合法代码集中任意两组合法代码之间对应二进制位不同的个数。
 选择码距必须考虑信息发生差错的概率和系统能容许的最小差错率。码距越大,抗干扰能力、纠错能力越强;码距越大,数据冗余越大,编码效率越低。2.4.2奇偶校验 选择码距必须考虑信息发生差错的概率和系统能容许的最小差错率。码距越大,抗干扰能力、纠错能力越强;码距越大,数据冗余越大,编码效率越低。2.4.2奇偶校验  - 发送方生成 校验码 = 原始数据 + 校验位p
- 接收方利用校验码生成 检错码G
- 奇校验检错码:

- G≠0表示数据发生错误,奇数位错?偶数位错?
- G=0是否表示数据正确? 能否纠错?
 计算机在进行大量字节(数据块)传送时,不仅每一个字节有一个奇偶校验位做横向校验,而且全部字节的同一位也设置一个奇偶校验位做纵向校验,这种横向、纵向同时校验的方法称为交叉奇偶校验。 计算机在进行大量字节(数据块)传送时,不仅每一个字节有一个奇偶校验位做横向校验,而且全部字节的同一位也设置一个奇偶校验位做纵向校验,这种横向、纵向同时校验的方法称为交叉奇偶校验。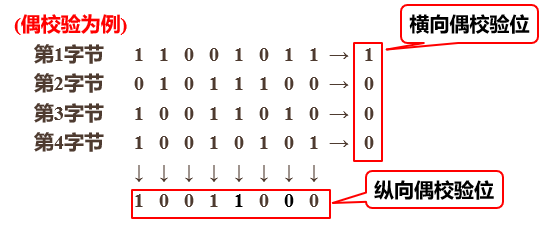    2.4.3海明校验 2.4.3海明校验       例题:设有一个8位信息为10101100,试求海明编码的生成和校验过程,并假设在没有3位错的情况下,尝试通过引入总偶校验位来区分一位错和两位错。(1)编码生成 例题:设有一个8位信息为10101100,试求海明编码的生成和校验过程,并假设在没有3位错的情况下,尝试通过引入总偶校验位来区分一位错和两位错。(1)编码生成 ∴可得到用二进制表示的海明码为: ∴可得到用二进制表示的海明码为: (2)接收方校验 假设传送后H5(D2)和 H6(D3)位发生了错误: (2)接收方校验 假设传送后H5(D2)和 H6(D3)位发生了错误: 举例: 举例: 特点: 特点: - 编码效率高:数据增加一倍,校验位只增加一位
- 可纠正一位错
- 50年代发明时用于自动处理穿孔卡片故障
- 现在普遍用于ECC DRAM芯片
- RAID2,卫星通讯
理解以本图为例  - 0001到1100是1-12的序号
- P1校验位是校验四位数中从右往左第一位的
- Pall是用来校验所有是否有错的
2.4.4CRC循环冗余校验
- 模2加减运算规则:异或运算,加不进位,减不借位
- 0±0=0,0±1=1,1±0=1,1±1=0
- 模2除——按模2减,求部分余数,不借位
- 部分余数首位为1时,上商1,减除数;
- 部分余数首位为0时,上商0,减0;
- 当余数的位数小于除数时得出余数。
习题1)[2015]由3个“1”和5个“0”组成的8位二进制补码,能表示的最小整数是BA.-126 B.-125 C.-32 D.-32)[2019]考虑以下 C 语言代码:unsigned short usi=65535 ;short si=usi ;执行上述程序段后,si的值是__A__。A.-1 B. -32767 C.-32768 D.-655353)[2012]假定编译器规定int和short类型长度分别为32位和16位,执行下列C语言语句: unsigned short x=65530; unsigned int y=x; 得到y的机器数为__B__A.0000 7FFAH B.0000 FFFAH C.FFFF 7FFAH D.FFFF FFFAH4) [2016]有如下C语言程序段: short si=-32767; unsigned short usi=si; 执行上述两条语句后,usi的值为___C___ A.-32767 B.32767 C.32768 D.327695)[2011]float型数据通常用IEEE 754单精度浮点数格式表示。若编译器将float型变量x分配在一个32位浮点寄存器FR1中,且x=-8.25,则FR1的内容是___A___  A.C104 0000H B.C242 0000H  C.C184 0000H  D.C1C2 0000H6)[2013]某数采用IEEE 754 单精度浮点数格式表示为C640 0000H,则该数的值是___A___A.-1.5×213 B. -1.5× 212 C.-0.5×213 D.-0.5×2127)[2012]float类型(即IEEE754 单精度浮点数格式)能表示的最大正整数是___C___A. 2126-2103 B. 2127-2104 C. 2127-2103 D.2128-21048)[2018]IEEE754单精度浮点格式表示的数中,最小规格化正数是___A___A.1.0×2-126 B.1.0×2-127 C.1.0×2-128 D.1.0×2-1499)[2014]float型数据通常用IEEE 754单精度浮点格式表示。假定两个float型变量x和y分别存放在32位寄存器f1和f2中,若(f1)=CC90 0000H,(f2)=B0C0 0000H,则x和y之间的关系为___A___A.x<y且符号相同 B.x<y且符号不同 C.x>y且符号相同 D.x>y且符号不同10)[2010]假定变量i、f、d的数据类型分别为int、float、double(int用补码表示,float和double用IEEE 754标准中的单精度和双精度浮点数据格式表示),已知i=785,f=1.5678e3,d=1.5e100,若在32位机器中执行下列关系表达式,则结果为真的是___B__ I.i==(int)(float)i II.f==(float)(int)f III.f==(float)(double)f IV.(d+f)-d==f A.仅I、II B.仅I、III C.仅II、III D.仅III、IV11)[2013]用海明码对长度为8位的数据进行检/纠错时,若能纠正一位错,则校验位数至少为__C__ A.2 B.3 C.4 D.5【2022年】32位补码所能表示的整数范围是( A) A. -232~231-1 B. -231~231-1 C. -232~232-1 D. -231~232-1 【2022年】-0.4375的 IEEE 754单精度浮点数表示为(A)A. BEEO 0000H B. BF60 0000H C. BF70 0000H D. C0E0 0000H【2021年】已知带符号整数用补码表示,变量x,y,z的机器数分别为FFFDH,FFDFH,7FFCH,下列结论中,正确的是(A)A.若x,y和z为无符号整数,则z<x<yB.若x,y和z为无符号整数,则x<y<zC.若x,y和z为带符号整数,则x<y<zD.若x,y和z为带符号整数,则y<x<z【2021年】下列数值中,不能用IEEE754浮点数格式精确表示的是(A)A. 1.2 B. 1.25 C. 2.0 D. 2.5【2020年】已知带符号整数用补码表示,float型数据用IEEE 754标准表示,假定变量x 的类型只可能是int或 float,当x的机器数为C800 0000H时,x的值可能是(A)A. -7x2 27 B. -2 16 C. 2 17 D. 25*2 27 章节作业1. 设X= —0.1011,则[x]补为(C)A. 1.1011B. 1.0100C. 1.0101D. 1.10012. 若[X]反=1.1011,则x=(B)A. -0.0101B. -0.0100C. 0.1011D. -0.10113. 定点8位字长的字,采用2的补码形式表示8位二进制整数,可表示的数范围为(D )A. -127~+127B. -2127~+2127C. -2-128~+2127D. -128~+1274. 一个8位二进制整数,若采用补码表示,且由4个1和4个0组成,则最小值为(D)A. -120B. -7C. -112D. -1215. 设X= -0.1011,则[X]补为(C)A. 1.1011B. 1.0100C. 1.0101D. 1.10016. 计算机机器数的表示方法中,零的表示方法唯一的是(D)A. 原码B. 补码C. 移码D. 补码和移码7. 零的原码可以用以下哪个代码表示(B)A. 11111111B. 10000000C. 01111111D. 110000008. 下列数中最小的数是(B)A. (1101001)2B. (52)8C. (133)8D. (30)169. 在整数定点机中,下述第(B)种说法是正确的­A. 原码和反码不能表示 -1,补码可以表示 -1;B. 三种机器数均可表示 -1;C. 三种机器数均可表示 -1,且三种机器数的表示范围相同;D. 三种机器数均不可表示 -1。10. 若某数x的真值为-0.1010,在计算机中该数表示为1.0110, 则该数所用的编码方法为(B)码A. 原B. 补C. 反D. 移11. 9位原码能表示的数据个数是 (C)A. 10B. 9C. 511D. 51212. 针对8位二进制数,下列说法中正确的是(B)A. -127的补码为10000000B. -127的反码等于0的移码C. +1的移码等于-127的反码D. 0的补码等于-1的反码13. n位二进制定点整数表示的最大值是(D)A. 2nB. 2n-1C. 2n-1D. 2n-1-114. 设寄存器内容为1111 1111,若它等于+127,则为(D)A. 原码B. 反码C. 补码D. 移码15. 对于定点机,下列说法错误的是(A)A. 除补码外,原码和反码不能表示-1B. +0的原码不等于-0的原码C. +0的反码不等于-0的反码D. 对于相同的机器字长,补码比原码和反码能多表示一个负数16. 在浮点数中,当数据的绝对值太小,以至于小于所能表示的数据时,称为浮点数的(A)A. 下溢B. 负下溢C. 负溢D. 正下溢17. 在规格化浮点数表示中, 保持其他方面不变, 将阶码部分的移码表示改为补码表示,将会使数的表示范围(C)A. 增大B. 减少C. 不变D. 以上都不对18. 采用规格化浮点数是为了(D)A. 增加数据的表示范围B. 方便浮点运算C. 防止运算时数据溢出D. 提高数据的表示精度19. 若浮点数用补码表示,则判断运算结果是否为规格化数的方法是(C)A. 阶符与数符相同为规格化数B. 阶符与数符相异为规格化数C. 数符与尾数小数点后第一位数字相异为规格化数D. 数符与尾数小数点后第一位数字相同为规格化数20. float型数据通常用IEEE754单精度数浮点数表示。 假定两个float型变量x和y分别存放在32位寄存器f1和f2中,若(f1)=CC90 0000H,(f2)=B0C0 0000H,则x和y的关系为(A)A. x<y,且符号相同B. x<y,且符号不同C. x>y,且符号相同D. x>y,且符号不同21. 表示浮点数时,若要求机器零在计算机中的表示全“0”,则阶码应采用的编码是(D)A. 原码B. 反码C. 补码D. 移码22. 已知大写英文字母A的ASCII码为41H,现字母F被存放某个存储单元中,若采用偶校验(假设最高位作为校验位),则该存储单元中存放的十六进制数据是 (B)A. 46HB. C6HC. 47HD. C7H23. 假定下列字符码中有奇偶校验位,但没有数据错误,采用偶校验的字符码是(A)A. 1100 1001B. 1101 0110C. 1100 0001D. 1100 101124. 若浮点数结果尾数不是规格化数,将进行结果规格化。结果规格化有左规和右规之分,下列操作中,属于结果规格化的操作是( B )Ⅰ. 尾数左移1位,阶码加1 Ⅱ. 尾数左移1位,阶码减1Ⅲ. 尾数右移1位,阶码加1 Ⅳ. 尾数右移1位,阶码减1A. Ⅰ、 ⅢB. Ⅱ、 ⅢC. Ⅰ、 ⅣD. Ⅱ、 Ⅳ25. 在整数定点机中,若寄存器的内容是80H, 当它分别代表原码、补码、反码、无符号数时, 所对应的十进制数值分别为_-0_、_-128_、_-127_、_128_26. 某8位寄存器中, 存放了一个机器数, 十六进制编码为80H,则:(1)如果它是补码表示的定点整数, 则它的十进制真值是_-128_(2)如果它是补码表示的定点小数, 则它的十进制真值是_-1_(3)如果它是反码表示的定点整数, 则它的十进制真值是_-127_(4)如果它是无符号整数,则它的十进制真值是_128_27. 若8位有效信息为01101101,海明码是_011001100111;1011001100111_28. 如果采用偶校验,0101010的校验位是_1_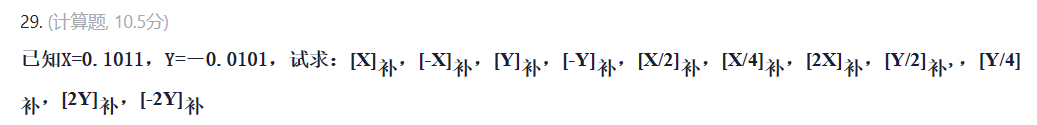 [X]补=0.1011;[-X]补=1.0101;[Y]补=1.1011;[-Y]补=0.0101;[X/2]补=0.0101(1);[X/4]补=0.0010(11);[2X]补=0.0110(溢出)[Y/2]补=1.1101(1);[Y/4]补=1.1110(11);[2Y]补=1.0110;[-2Y]补=0.1010 [X]补=0.1011;[-X]补=1.0101;[Y]补=1.1011;[-Y]补=0.0101;[X/2]补=0.0101(1);[X/4]补=0.0010(11);[2X]补=0.0110(溢出)[Y/2]补=1.1101(1);[Y/4]补=1.1110(11);[2Y]补=1.0110;[-2Y]补=0.1010 [-35]原=10100011 [127]原=01111111 [-127]原=11111111 [-1]原=10000001[-35]反=11011100 [127]反=01111111 [-127]反=10000000 [-1]反=11111110[-35]补=11011101 [127]补=01111111 [-127]补=10000001 [-1]补=11111111[-35]移=01011101 [127]移=11111111 [-127]移=00000001 [-1]移=01111111 [-35]原=10100011 [127]原=01111111 [-127]原=11111111 [-1]原=10000001[-35]反=11011100 [127]反=01111111 [-127]反=10000000 [-1]反=11111110[-35]补=11011101 [127]补=01111111 [-127]补=10000001 [-1]补=11111111[-35]移=01011101 [127]移=11111111 [-127]移=00000001 [-1]移=01111111 IEEE754标准32位浮点的规格化数为:真值X=(-1)s×1.M×2E-127.其中S是符号;E是偏置后的阶码;M是尾数,e是阶码(1)首先转换成二进制数: 27/64=27/26=(0.011011)2=(-1)0×1.1011×2-2所以,S=0,E=-2+127=125=(111 1101)2,M=1011。故32位的规格化浮点数为:00111110 11011000 00000000 00000000,即十六进制的(3ED80000)16(2)-27/64=-(1.1011)2 ×2-2=(-1)1×1.1011×2-2 所以,S=1,E=e+127=125=(0111 1101)2,M=1011 32位的规格化浮点数为: 10111110 11011000 00000000 00000000,即十六进制的(BED80000)16 IEEE754标准32位浮点的规格化数为:真值X=(-1)s×1.M×2E-127.其中S是符号;E是偏置后的阶码;M是尾数,e是阶码(1)首先转换成二进制数: 27/64=27/26=(0.011011)2=(-1)0×1.1011×2-2所以,S=0,E=-2+127=125=(111 1101)2,M=1011。故32位的规格化浮点数为:00111110 11011000 00000000 00000000,即十六进制的(3ED80000)16(2)-27/64=-(1.1011)2 ×2-2=(-1)1×1.1011×2-2 所以,S=1,E=e+127=125=(0111 1101)2,M=1011 32位的规格化浮点数为: 10111110 11011000 00000000 00000000,即十六进制的(BED80000)16 IEEE754标准32位浮点的规格化数为:X=(-1)s×1.M×2E-127.其中S是符号;E是偏置后的阶码;M是尾数,e是阶码(1) 1 10000011 110 0000 0000 0000 0000 0000S=1E=(10000011)2=131 e=E-127=131-127=41.M=(1.11)2所以,该浮点数为 (-1)1×1.11×24=-(11100)2=-28(2) 0 01111110 101 0000 0000 0000 0000 0000S=0E=(01111110)2=126 e=E-127=126-127=-11.M=(1.101)2所以,该浮点数为 (-1)1×(1.101)2×2-1=(0.1101)2=0.8125 IEEE754标准32位浮点的规格化数为:X=(-1)s×1.M×2E-127.其中S是符号;E是偏置后的阶码;M是尾数,e是阶码(1) 1 10000011 110 0000 0000 0000 0000 0000S=1E=(10000011)2=131 e=E-127=131-127=41.M=(1.11)2所以,该浮点数为 (-1)1×1.11×24=-(11100)2=-28(2) 0 01111110 101 0000 0000 0000 0000 0000S=0E=(01111110)2=126 e=E-127=126-127=-11.M=(1.101)2所以,该浮点数为 (-1)1×(1.101)2×2-1=(0.1101)2=0.8125 |
|
 发表于 2024-3-5 12:50
发表于 2024-3-5 12:50
 发表于 2024-3-5 19:37
发表于 2024-3-5 19:37
 发表于 2024-3-5 20:33
发表于 2024-3-5 20:33