【人工智能系列教程】机器学习(二)——单变量线性回归
本帖最后由 GodStick 于 2019-7-22 19:28 编辑> 从这一期就会有很多数学知识了,但是我换了一个图床,不知道会不会显示出来,如果显示不出来我再做替换吧。
#### 例题
为了让大家更加直观的理解这个模型,我们引入一个例题,我们有一组波特兰市的城市住房的价格数据,我们要通过这些数据来找出一个函数,来预测任意面积下的房价,这就是一个简单的线性回归问题。
这里给出的数据是一组房子面积对应的房价
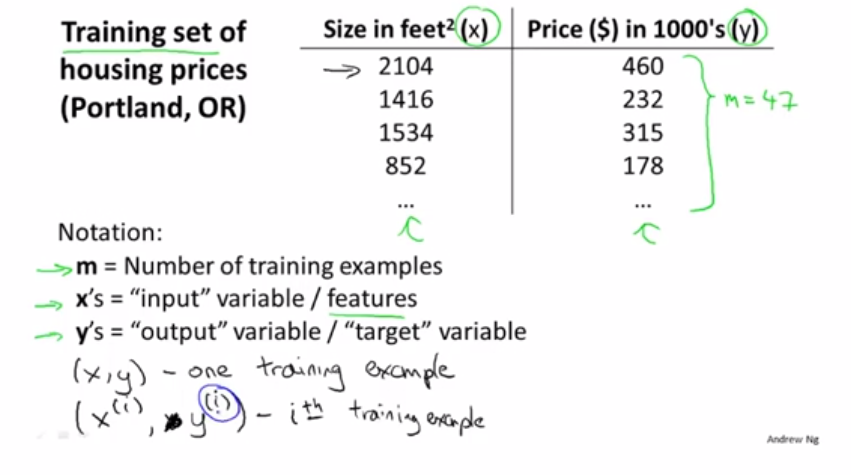
其中m代表训练集,x是输入,y是输出。我们用(x,y)来代表一个训练集,(x^i,y^i)代表第i行训练数据,比如x^2=2104.
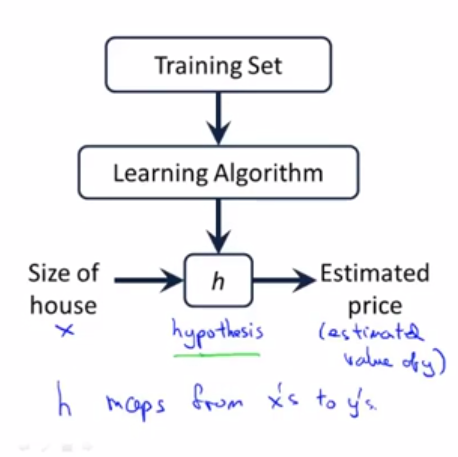
我们训练的目的就是让我们假设一个函数h,使这个函数拟合我们的数据集。
#### 代价函数
我们首先假设函数h(x)= θ0 + θ1x,其中θ0,θ1是这个模型需要变化的参数,我们主要就是训练这两个参数,让函数能达到我们预期的输入输出效果。
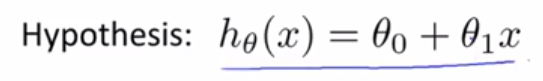
那么如何直观的表现出这个函数的拟合度呢,也就是这个函数的正确度,我们这里就引入了代价函数的概念。
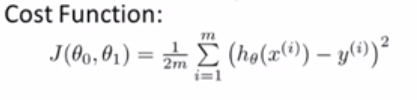
代价函数就是我们函数的输出值和相对应的真实值的方差,我们归回的目的就让方差最小化。
#### 梯度下降
既然我们的目的已经明确了,就是让代价函数最小化,我们怎么才能达到这个目的呢, 我们这里使用梯度下降的方法来达到这个目的,这个方法被广泛应用到机器学习领域之中。梯度下降原理很简单,就是不停的改变θ0,θ1的值,让代价函数得到最小值或者局部最小值。首先我们来看看梯度下降是如何工作的:
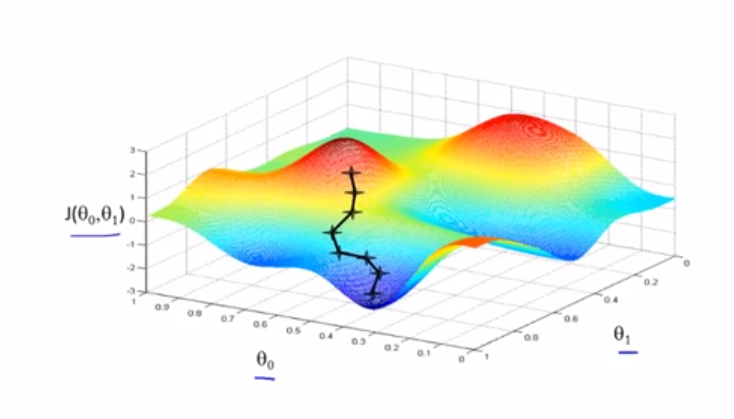
这是一个代价函数的图像,首先我们先初始赋值θ0,θ1,在上图的位置标注好了。然后从这个点出发,不断的找到下降的方向,一步一步的下降,直到走到无法继续下降位置。此时的θ0,θ1值就是代价函数的最小值或者是局部最小值。
那么怎么用数学公式来表达这个梯度下降的过程呢,其实很简单,只要用这个公式就行了:

这个就是传说中的梯度下降公式,其实原理很简单,就是让参数等于这个参数减去学习率乘于参数的偏导。但要注意的是两个参数的值要同时变化,这个`:=`号是赋值的意思,不是等于号!!!。如何理解这个公式呢?我们可以选择删去一个参数,只用一个参数来梯度下降,来看一下这个公式的工作原理:
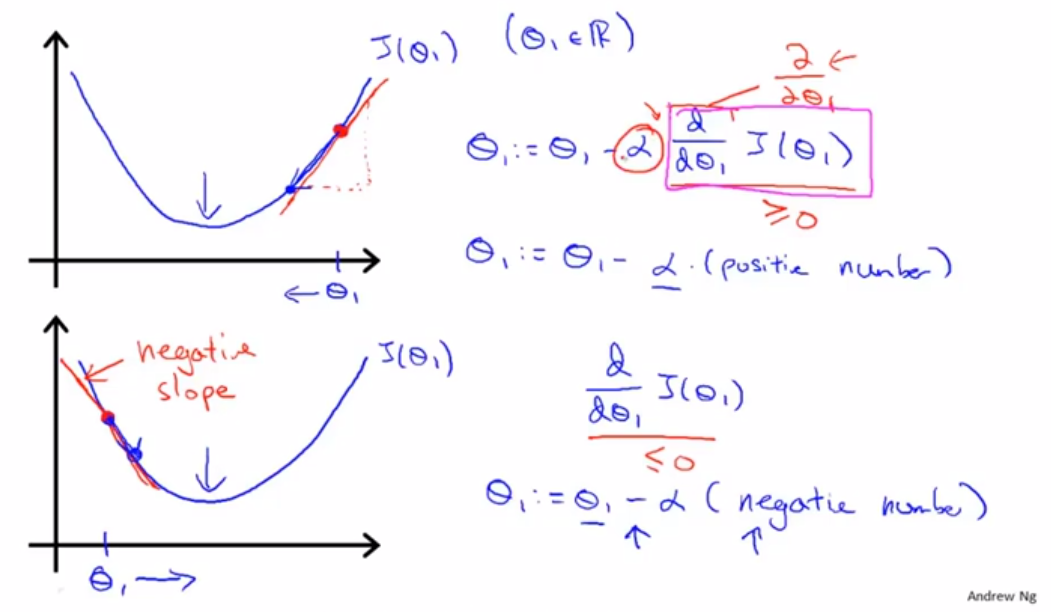
首先假如我们初始赋值在图中位置,我们运用公式。这个偏导数就是这一点在函数中的斜率,我们用斜率来乘于学习率(待会我们再解释这个学习率),再用原θ1的值减去这个乘积,我们可以发现,其实就是向函数下降的方向走了一步,这个学习率就是我们走的一步的长度,学习率大,我们一步下降的就多,斜率大我们下降的也多,但是总的来看下降的步长还是看学习率,应为越是快到最小值,我们的斜率就越小,我们下降的就越慢,当到达最小值的时候,斜率就等于零,参数就停止移动了。我们可以看出图片上面给了当θ1大于或者小于最小值的情况下公式的运算情况,有兴趣的可以自己一步一步的计算试试看。
#### 后记
通过我们得出的公式,你可以用完成一个完整的回归模型。接下来的笔记我会带大家学习,多个x输入情况下的回归建立。 人工智能:
从样本数据中挖掘规律。根据规律预测未来数据。
规律是什么?
把数据看作随机变量,用分布函数可以完整地描述随机变量的统计规律。
找一个合理的分布函数,就是挖掘规律。
怎么找分布函数?
根据贝叶斯定理(条件概率公式),样本数据作为先验分布信息,设计一个参数可变的模型函数(似然函数)。
先验分布信息和似然函数结合起来,从而求得合理的模型参数,得到后验分布,并使用后验分布(的期望)作为 预测模型
求解后验分布是一件很难的事情,给出了先验分布和似然函数后,并不一定能把后验分布求解出来(比如要进行积分,而这个积分积不出)
只有在一些特殊情况下,能够把后验分布求出来,比如当先验分布与似然函数“共轭”时,求解后验分布就容易了。
设计学习模型时尽可能优先选共轭似然函数。
二项分布(Binomial distribution)Beta分布
多项式分布(Multinomial distribution) 狄利克雷分布(Dirichlet distribution)
高斯分布 高斯分布
那么当先验分布与似然函数“不共轭”时,后验分布无法直接计算得到时,怎么办?
一种合理的想法就是对后验分布进行近似,既然求不出“精确表达式”,那就用“近似表达式”呗。这里,主要有三种近似的策略:
①后验分布中包含了模型参数,使用 点估计(point estimate--the MAP solution) 方法对模型参数进行估计。这方法用到了牛顿法,首先选择一个初始点,然后通过偏导数不断选择下一个点更新初始点,直到偏导数等于0,最终得到极值。当样本的特征是多维的时,就是使用Hessian矩阵来更新了。
显然,这是一种不断迭代的思路。因此,该方法需要考虑“收敛性”问题---最终能不能得到最值(极值)?要迭代多少次才能收敛?收敛得快不快?
能不能收敛到最优值,可以根据Hessian矩阵的正定性(负定性)来判断,收敛得快不快则需要根据实际情况具体分析了。
②在“点估计”近似方法中,是直接针对模型的参数进行点估计,没有牵涉到 后验分布函数,而Laplace近似方法就是对后验分布函数进行近似。
前面提到,我们无法精确求得后验分布函数,那可以找一个 与 后验分布 相似的函数,用它来作为我们的后验分布函数就行了。这称为Laplace approximation.
这里的Laplace近似的基本思路就是,先将后验分布表示成Log函数的形式,然后使用泰勒展开对Log函数展开到二阶,由于我们需要最大化后验分布函数,那么一阶泰勒展开项为0,而二阶展开项,则使用高斯分布来近似表示。对于高斯分布而言,需要选择一个合理的均值和方差,具体如何选择的细节就不说了。(我也不知道)
③Sample techniques,该方法的思路是使用Metropolis-Hastings算法 直接对原样本数据进行近似。与方法②的区别是:方法②是对描述样本数据的分布函数进行近似,这Sample Techniques是直接对数据进行近似。
最大后验估计可以用以下几种方法计算:
解析方法,当后验分布的模能够用解析解方式表示的时候用这种方法。当使用共轭先验的时候就是这种情况。
通过如共扼积分法或者牛顿法这样的数值优化方法进行,这通常需要一阶或者导数,导数需要通过解析或者数值方法得到。
通过期望最大化算法的修改实现,这种方法不需要后验密度的导数。
北上飞 发表于 2019-7-22 19:45
我记得我们高中的时候学过一些内容
高数中的导数概念在高中是有学的 支持 加油呀 支持大佬 真在学习中:lol 我记得我们高中的时候学过一些内容 感谢分享经验,可以多多发帖试试
支持大佬,认真学习中!! 没有Python基础,不知道能不能学会
其实我也是高中生哎
向大佬学习,很多不懂但是不妨碍我百度一下意思去学习
页:
[1]
2