【人工智能系列教程】机器学习（二）——单变量线性回归

GodStick

从这一期就会有很多数学知识了，但是我换了一个图床，不知道会不会显示出来，如果显示不出来我再做替换吧。

例题

为了让大家更加直观的理解这个模型，我们引入一个例题，我们有一组波特兰市的城市住房的价格数据，我们要通过这些数据来找出一个函数，来预测任意面积下的房价，这就是一个简单的线性回归问题。

这里给出的数据是一组房子面积对应的房价

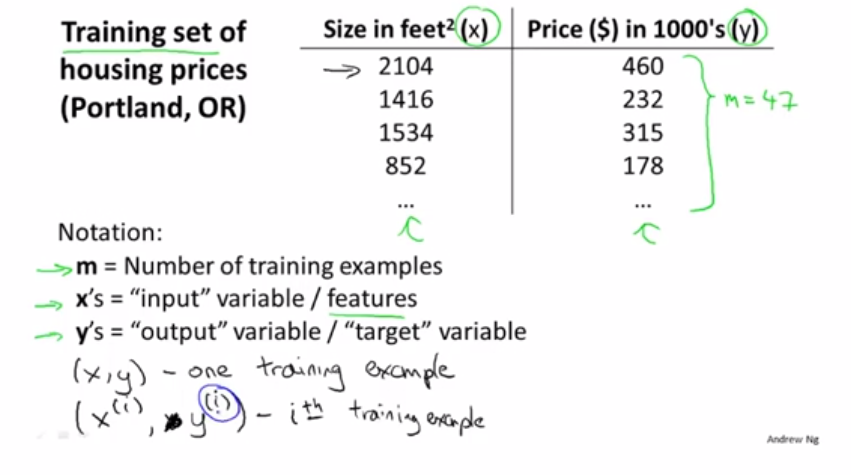
其中m代表训练集，x是输入，y是输出。我们用（x,y）来代表一个训练集，(x^i,y^i）代表第i行训练数据，比如x^2=2104.

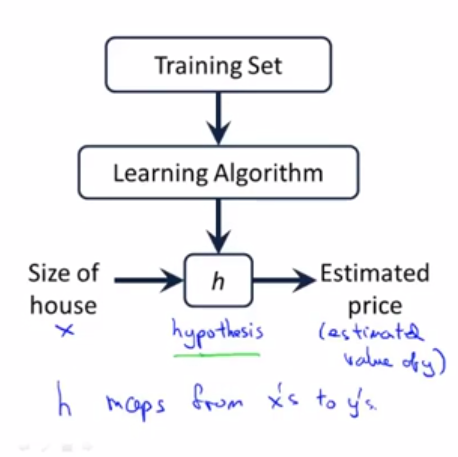
我们训练的目的就是让我们假设一个函数h,使这个函数拟合我们的数据集。

代价函数

我们首先假设函数h（x）= θ0 + θ1x，其中θ0，θ1是这个模型需要变化的参数，我们主要就是训练这两个参数，让函数能达到我们预期的输入输出效果。

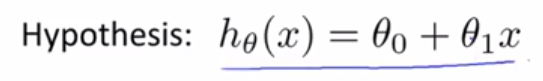
那么如何直观的表现出这个函数的拟合度呢，也就是这个函数的正确度，我们这里就引入了代价函数的概念。

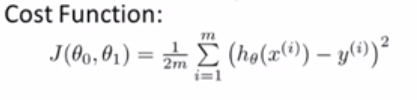
代价函数就是我们函数的输出值和相对应的真实值的方差，我们归回的目的就让方差最小化。

梯度下降

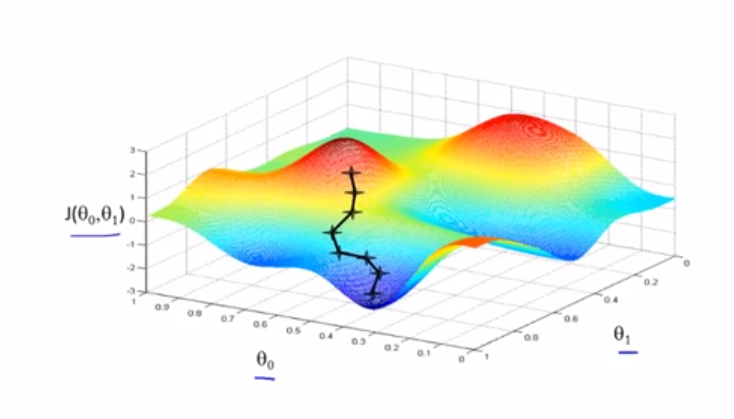
既然我们的目的已经明确了，就是让代价函数最小化，我们怎么才能达到这个目的呢， 我们这里使用梯度下降的方法来达到这个目的，这个方法被广泛应用到机器学习领域之中。梯度下降原理很简单，就是不停的改变θ0，θ1的值，让代价函数得到最小值或者局部最小值。首先我们来看看梯度下降是如何工作的：

这是一个代价函数的图像，首先我们先初始赋值θ0，θ1，在上图的位置标注好了。然后从这个点出发，不断的找到下降的方向，一步一步的下降，直到走到无法继续下降位置。此时的θ0，θ1值就是代价函数的最小值或者是局部最小值。

那么怎么用数学公式来表达这个梯度下降的过程呢，其实很简单，只要用这个公式就行了：

这个就是传说中的梯度下降公式，其实原理很简单，就是让参数等于这个参数减去学习率乘于参数的偏导。但要注意的是两个参数的值要同时变化，这个:=号是赋值的意思，不是等于号！！！。如何理解这个公式呢？我们可以选择删去一个参数，只用一个参数来梯度下降，来看一下这个公式的工作原理：

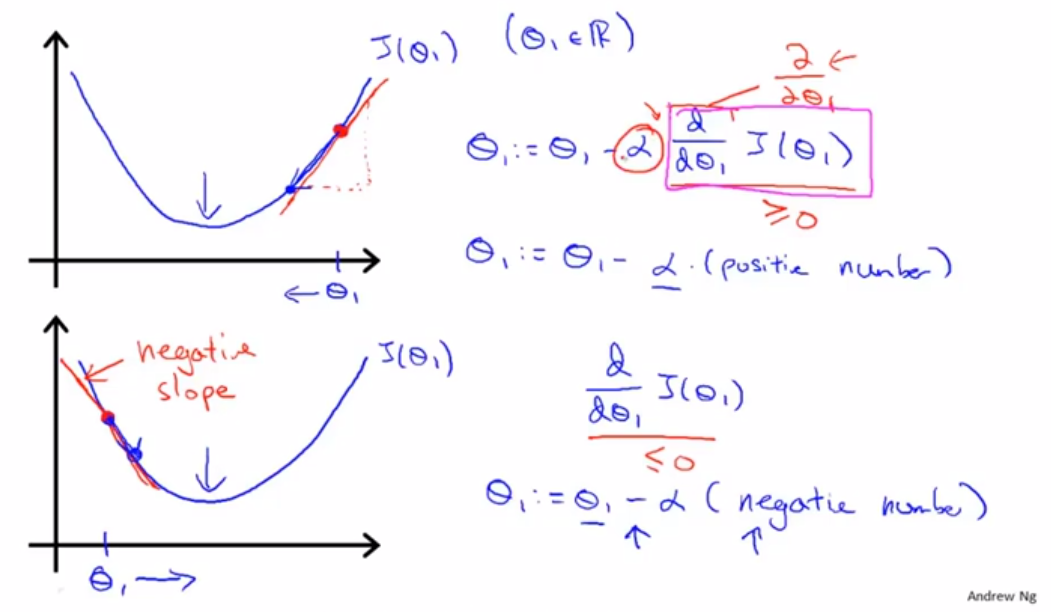
首先假如我们初始赋值在图中位置，我们运用公式。这个偏导数就是这一点在函数中的斜率，我们用斜率来乘于学习率（待会我们再解释这个学习率），再用原θ1的值减去这个乘积，我们可以发现，其实就是向函数下降的方向走了一步，这个学习率就是我们走的一步的长度，学习率大，我们一步下降的就多，斜率大我们下降的也多，但是总的来看下降的步长还是看学习率，应为越是快到最小值，我们的斜率就越小，我们下降的就越慢，当到达最小值的时候，斜率就等于零，参数就停止移动了。我们可以看出图片上面给了当θ1大于或者小于最小值的情况下公式的运算情况，有兴趣的可以自己一步一步的计算试试看。

后记

通过我们得出的公式，你可以用完成一个完整的回归模型。接下来的笔记我会带大家学习，多个x输入情况下的回归建立。

KARMA07007

人工智能：
从样本数据中挖掘规律。根据规律预测未来数据。

规律是什么?
把数据看作随机变量，用分布函数可以完整地描述随机变量的统计规律。
找一个合理的分布函数，就是挖掘规律。
怎么找分布函数？
根据贝叶斯定理（条件概率公式），样本数据作为先验分布信息，设计一个参数可变的模型函数（似然函数）。
先验分布信息和似然函数结合起来，从而求得合理的模型参数，得到后验分布，并使用后验分布(的期望)作为 预测模型

求解后验分布是一件很难的事情，给出了先验分布和似然函数后，并不一定能把后验分布求解出来（比如要进行积分，而这个积分积不出）
只有在一些特殊情况下，能够把后验分布求出来，比如当先验分布与似然函数“共轭”时，求解后验分布就容易了。
设计学习模型时尽可能优先选共轭似然函数。

二项分布（Binomial distribution）Beta分布
多项式分布（Multinomial distribution） 狄利克雷分布（Dirichlet distribution）
高斯分布 高斯分布

那么当先验分布与似然函数“不共轭”时，后验分布无法直接计算得到时，怎么办？
一种合理的想法就是对后验分布进行近似，既然求不出“精确表达式”，那就用“近似表达式”呗。这里，主要有三种近似的策略：
①后验分布中包含了模型参数，使用 点估计(point estimate--the MAP solution) 方法对模型参数进行估计。这方法用到了牛顿法，首先选择一个初始点，然后通过偏导数不断选择下一个点更新初始点，直到偏导数等于0，最终得到极值。当样本的特征是多维的时，就是使用Hessian矩阵来更新了。
显然，这是一种不断迭代的思路。因此，该方法需要考虑“收敛性”问题---最终能不能得到最值(极值)？要迭代多少次才能收敛？收敛得快不快？
能不能收敛到最优值，可以根据Hessian矩阵的正定性(负定性)来判断，收敛得快不快则需要根据实际情况具体分析了。
②在“点估计”近似方法中，是直接针对模型的参数进行点估计，没有牵涉到 后验分布函数，而Laplace近似方法就是对后验分布函数进行近似。
前面提到，我们无法精确求得后验分布函数，那可以找一个 与 后验分布 相似的函数，用它来作为我们的后验分布函数就行了。这称为Laplace approximation.
这里的Laplace近似的基本思路就是，先将后验分布表示成Log函数的形式，然后使用泰勒展开对Log函数展开到二阶，由于我们需要最大化后验分布函数，那么一阶泰勒展开项为0，而二阶展开项，则使用高斯分布来近似表示。对于高斯分布而言，需要选择一个合理的均值和方差，具体如何选择的细节就不说了。(我也不知道)
③Sample techniques，该方法的思路是使用Metropolis-Hastings算法 直接对原样本数据进行近似。与方法②的区别是：方法②是对描述样本数据的分布函数进行近似，这Sample Techniques是直接对数据进行近似。

最大后验估计可以用以下几种方法计算：
解析方法，当后验分布的模能够用解析解方式表示的时候用这种方法。当使用共轭先验的时候就是这种情况。
通过如共扼积分法或者牛顿法这样的数值优化方法进行，这通常需要一阶或者导数，导数需要通过解析或者数值方法得到。
通过期望最大化算法的修改实现，这种方法不需要后验密度的导数。

GodStick

北上飞 发表于 2019-7-22 19:45
我记得我们高中的时候学过一些内容

高数中的导数概念在高中是有学的

KARMA07007

支持 加油呀

IMF

支持大佬 真在学习中

北上飞

我记得我们高中的时候学过一些内容

努力的小七

感谢分享经验，可以多多发帖试试

yunzha1

支持大佬，认真学习中！！

未晴雾香

没有Python基础，不知道能不能学会
其实我也是高中生哎

lsy832

向大佬学习，很多不懂但是不妨碍我百度一下意思去学习