说明
Chaos Emulator是目前我个人开发的一个引力模拟器。项目的背景说明请看v0.2.3发布介绍。我将在这篇文章中对这个模拟器的重要版本进行详细说明。相关的代码发布见代码库。
初次搭建：v0.1.0
对于Chaos Emulator的构想是从Osmos引申出来的。我在v0.1.0的初始版本中构想它是一个二维的物理沙盒，并且能够对星体的运动和引力进行精确的模拟，并且产生连贯的动画输出，甚至可以通过键盘和鼠标输入，在某个时间点对星体的坐标、质量等参数进行修改，以达到特定的运动状态。
我未曾接触C++的图形动画库，所以暂用Python语言和Python的第三方图形库PyGame作为引力模拟器的实现工具。然后，快速地编写如下的最简框架：
import pygame, math
pygame.init()
s = pygame.display.set_mode([1300, 800], pygame.RESIZABLE)
flag = True
while flag:
for evt in pygame.event.get():
if evt.type == pygame.QUIT:
flag = False
pygame.quit()
程序首先实现一个最基础的PyGame窗口。import模块包括绘图库PyGame和数学库math，数学库在将来的引力计算等核心代码中会被用到。
创建窗口对象s，描述为一个1300*800的简单窗口，可以调整尺寸。
然后，初始化窗口的响应循环，在循环中包含一个事件处理的for循环，一旦发现窗口退出事件，将在该次循环结束后终止运行。然后，程序调用quit方法退出PyGame运行环境。
接下来可以开始考虑星体了。
根据我的设想，目前先添加如下两个星体的坐标：
ATTR = [600, 400] # 吸引体的坐标
pos = [300, 300] # 伴星的坐标
目前为了便于实现，吸引体不受引力的相互作用，并且设置其水平和横向速度为0，即为静止，所以目前不考虑它的任何运动。
对于伴星，需要考虑它的运动状态，所以为它添加一个表示速度的数对
speed = [0, 200]
速度并不带具体的单位，在此版本中它代表每一帧计算中星体应当沿水平方向和垂直方向移动的像素数。
接下来，定义一个FPS——帧速率的具体控制值：FPS = 25
然后，再根据秒数1和FPS的值计算出每帧保留的时间长短，单位为秒，记为SECT：SECT = 1 // FPS，这个值用于时钟延时的参数传入，并且作为一个简单的时间尺度值。
接下来可以实现时钟延时。在flag = True之后插入一行代码：
clock = pygame.time.Clock()创建时钟对象
然后在循环体的事件捕捉之后加入：
clock.tick(SECT)进行延时。
接下来是最核心的代码。
在此版本中，尚未估测运行逼真的万有引力公式是否会达到上限。因此，此时将引力值默认一个定值参数，引力与星体间的距离无关。
循环体内数据更新代码如下：
xf = 1
if ATTR[0] < pos[0]: xf = -1
yf = 1
if ATTR[1] < pos[1]: yf = -1
try:
speed[0] += 3 * xf
speed[1] += 3 * yf
except ZeroDivisionError:
pass
pos[0] += speed[0] / SECT
pos[1] += speed[1] / SECT
xf和yf是位置指标，仅用于判断吸引体与伴星的上下、左右关系，以便进行方向正确的引力模拟。然后，向速度叠加引力影响。try-except语句是调试遗留代码，为了应对特殊的bug而保留，后续版本中会修改或删除。
最后，根据更新后的速度更新伴星的坐标。
在这段代码前面添加如下的绘制脚本：
tpos = [math.floor(pos[0] + 0.5),math.floor(pos[1] + 0.5)]
s.fill([0, 0, 0])
pygame.draw.circle(s, (255, 255, 255), tpos, 10)
pygame.draw.circle(s, (255, 0, 0), ATTR, 10)
pygame.display.flip()
最终渲染的效果如下：
红色的吸引体吸引白色的伴星绕其运动。禁止擦除后，可以看到它的轨迹变化非常规则，这一定程度上是由于不逼真的引力计算：
引力公式将在后续版本中改进。
双星体相互作用：v0.1.1
这个版本的主要更新是将吸引体变为受引力影响且具有速度的星体。
为其添加速度和更新代码：
speed2 = [-300, -300]
xf = 0
if pos1[0] < pos2[0]: xf = -1
if pos1[0] > pos2[0]: xf = 1
yf = 0
if pos1[1] < pos2[1]: yf = -1
if pos1[1] > pos2[1]: yf = 1
try:
speed2[0] += 2 * xf
speed2[1] += 2 * yf
except ZeroDivisionError:
pass
与v0.1.1的伴星计算方法相同。
修改渲染的方法，具体不再赘述。
以下是此版本禁用刷新之后的运动轨迹效果：
质量与星体半径尚未采用特定公式计算。
v0.1.2：初次尝试万有引力公式
这个版本的核心更新就是引入实现万有引力公式计算的函数。
def calc(x1, x2, y1, y2, r1, r2):
dist = ((x1-x2)**2+(y1-y2)**2)
res = g ** 2 * r1 * r2 / dist
if dist < r1 + r2:
res /= dist * g
if dist < 1:
res = 0
return res
该函数输入两星体质心位置和两星体的质量（质量和半径通用变量r1和r2计算），计算出质心距和两星体质量之积后，代入万有引力公式：
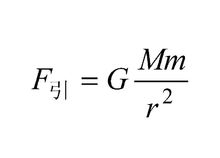
进行计算。
函数为了克服质心距过小时引力无限大的超出适用范围的无效计算结果，检测两星体距离，距离过近时会沿用上一帧的引力大小，以保证避免失误。
下图为引入万有引力计算功能后的轨迹，可以看出两星绕共同点旋转时出现的轨迹偏差程度有明显降低。
v0.2.0：转变为弹球模式
过强的引力和不变的轨迹有些时候让我觉得无聊，所以我打算根据Osmos的规则，将模拟器的星体变成弹球，在全屏模式下碰撞运动，作为一个屏保。
首先，将力处理部分的代码抽题出来，形成了一个专门的函数。涉及封装的东西在这里不多说。以下是检测碰撞并将速度方向取反的代码：
if obj2[0] + r2 > SIZE[0]: speed2[0] = -abs(speed2[0])
elif obj2[0] - r2 < 0: speed2[0] = abs(speed2[0])
if obj2[1] + r2> SIZE[1]: speed2[1] = -abs(speed2[1])
elif obj2[1] - r2< 0: speed2[1] = abs(speed2[1])
if obj1[0] + r1> SIZE[0]: speed1[0] = -abs(speed1[0])
elif obj1[0] - r1< 0: speed1[0] = abs(speed1[0])
if obj1[1] + r1> SIZE[1]: speed1[1] = -abs(speed1[1])
elif obj1[1] - r1< 0: speed1[1] = abs(speed1[1])
吸引体和伴星均会被限制在屏幕内。然后，就可以把重力系数调低，该版本中调成了较适合的系数g = 50.这样子，大部分情况下相互引力不会让星体处于稳定状态，但也无需担心星体逃逸而飞离屏幕。在反弹发生时，“完美边框”不会减损星体的动能。
此外，该版本中我参照Osmos的渲染效果，自己做了一个简陋的渲染优化——用三个同心圆依次叠加，形成两个看起来一样的星体。到了这一步，吸引体和伴星就几乎没有区别了，它们的形象在该版本中一致。
以下是渲染代码：
s.fill([0, 0, 0])
pos1 = [int(obj1[0] + 0.5), int (obj1[1] + 0.5)]
pos2 = [int(obj2[0] + 0.5), int (obj2[1] + 0.5)]
pygame.draw.circle(s, c1, pos1, int(r1))
pygame.draw.circle(s, c2, pos1, int(r1 / 1.4))
pygame.draw.circle(s, c3, pos1, int(r1 / 10))
pygame.draw.circle(s, c1, pos2, int(r2))
pygame.draw.circle(s, c2, pos2, int(r2 / 1.4))
pygame.draw.circle(s, c3, pos2, int(r2 / 10))
pygame.display.flip()
此版本的最终效果如图所示：
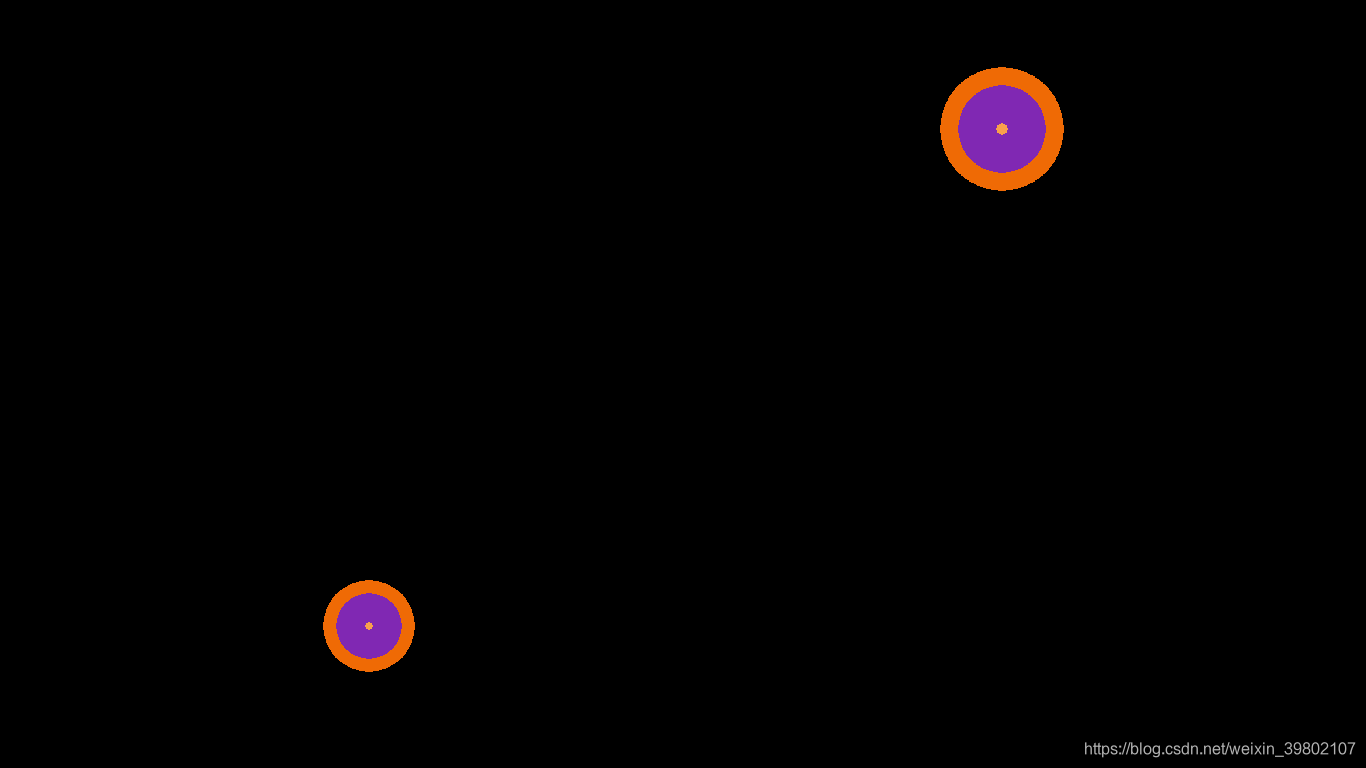
该截屏取于全屏模式下的程序界面。星体的运动模式基本上与上一版本一致，但总是被限制在屏幕框中。星体会互相吸引，也会由于自身惯性而逃逸。此版本的星体还不能相互碰撞和吸收，但该版本的模拟器已经成为一个良好的屏保程序，具有令人上瘾的观赏价值。完整代码比较长，代码仓库中有保存。
v0.2.1-0.2.3：最近阶段
由于自身学习和工作，模拟器的业余项目到最新版本（v0.2.3）之后就未持续进行。v0.2.1-0.2.3除了加入碰撞和吸收算法之外，没有对程序逻辑的实际修改，只进行了渲染的提升。
碰撞和吸收的算法是一项重要的功能，大部分的模拟器都会有这个功能。在最近阶段中，默认让吸引体吸收伴星。
为了确保碰撞和吸收不会对算法产生鲁棒性威胁，我在构建过程中修改了不少次代码。我还添加了星体被吸收后重生的脚本，以便减少手动操作的麻烦事。但是这样一来就有问题——吸引体会不断吸收然后质量变大。所以我陆续添加了A、D、←、→、S五个键盘操作，用于修改两星体的质量，并实时更新它们的半径。
然后是碰撞算法。我曾经企图通过两弧围成形状公式来求出两星体的重合部分，然后将重合的质量由一方转让给另一方。但是后来发现这不可行，于是只能可怜地枚举它们的重合部分，后来还给该功能打了N个条件补丁，以增强鲁棒性。
碰撞和吸收计算的核心代码如下：
if r1+r2+10 > dist: # 两星体相撞，目前默认由星体2号吸收1号
#if dist < min(r1, r2):
# speed1, speed2 = [0, 0], [0, 0] # 这里改成使用last的表达式
s = (r1+r2 - dist) / 4# 粗略计算重合的部分线段长
# 目标：将距离s一部分留给1号，另一部分被2号吸收，并最终使两星体相切，即r1+r2==dist
#d1 = ((m1-m2) + math.sqrt((m1-m2)**2 + min(dist, m1))) / 2
rawdm = 0.5*s * (r1+r2) if 0.5*s * (r1+r2) < m1 else m1 # 粗略计算被吸收的物质质量
dm = 0
#m2 += dm; m1 -= dm
#newm1, newm2 = m1, m2
while m1 >= 0 and m2 >= 0 and dm <= rawdm * 4:
m2 += 1; m1 -= 1; dm += 1
if not (m1 >= 0 and m2 >= 0): break
r1 = getr(m1); r2 = getr(m2)
if abs(dist-(r1+r2)) <= 5: break
if m1 < 0: m1 = 0
ns2 = []
#ns1, ns2 = [], []
#ns1.append((speed1[0]*m1 + speed2[0]*dm/max(m1, 1)) / (m1+dm))
#ns1.append((speed1[1]*m1 + speed2[1]*dm/max(m1, 1)) / (m1+dm))
ns2.append((speed2[0]*m2 + speed1[0]*dm) / (m2+dm))
ns2.append((speed2[1]*m2 + speed1[1]*dm) / (m2+dm))
#ns2.append((speed2[0]*m2 + speed1[0]*dm/max(m1, 1)) / (m2+dm))
#ns2.append((speed2[1]*m2 + speed1[1]*dm/max(m1, 1)) / (m2+dm))
speed2 = ns2
#speed1, speed2 = ns1, ns2
r1 = getr(m1) if m1 > 0 else 0
r2 = getr(m2) if m2 > 0 else 0
#print(m1, m2, m1+m2)
#if r1 < 0: return 'quit'
总之，现在的感觉是写得有点啰嗦。但是好处是，该方法是可行的。实际上，我对于当初怎么想的也有点忘了。两星体碰撞时，用该代码计算得到的转让质量还算正确，但是当吸收星体的质量小于被吸收星体的质量时，这个方法就需要优化了，目前对于该情况这个方法会出现计算不精确的问题。
另外，我被Osmos吸引的原因在于它精美的图形画质。虽然我用Python肯定达不到人家用C++的渲染效果，但是绘制点基础渐变还是可以的。所以尝试了一下，得到渐变的代码。
def fill(center, rs, re, cs, ce): # 绘制环形渐变，rs > re
'''默认为20层渐变'''
pygame.draw.circle(s, cs, center, rs)
dr = (re - rs) / 20
dcr = (ce[0] - cs[0]) / 20
dcg = (ce[1] - cs[1]) / 20
dcb = (ce[2] - cs[2]) / 20
for i in range(1, 19):
pygame.draw.circle(s, (int(cs[0] + dcr*i), int(cs[1] + dcg*i), int(cs[2] + dcb*i)), center, int(rs + dr*i))
pygame.draw.circle(s, ce, center, re)
最终，总体的效果还不错，只是内部留下了不少奇怪的变量，只待到时候重写和模块化时处理了……
如图即为目前成品效果，蓝色锥形轨迹是在吸引体吸收伴星时产生的。可以通过A、D键调节吸引体质量，S键将吸引体质量设为和伴星质量相等，←、→键调节伴星的质量。
致谢
感谢Osmos游戏和它的开发者（之一），Eddy Boxerman，对我进行了耐心帮助。
吾爱游客
发表于 2019-8-25 14:52
发表于 2019-8-26 11:50
