好的面试官能够能好的和面试者互动，而一场好的面试也能带给面试者更多的思考
面试题：有 N 个数，求能够组成最大值的 n-1 个数，不能使用除法
面试官给我出题后的 1 分钟内，我给出了第一种思路：排序。
将数字按升序排序，去除最小的那个数即可。
存在问题：时间复杂度高，只考虑了正数的情况。
面试官给出了第一次提示时间复杂度过高，要求降低时间复杂度。
这里其实已经把思考的范围缩小了，因为之前的排序时间度大概为 O(nlogn) （可参照快排和归并排序均摊时间复杂度），那要降低的话就是 O(n) 了，即在线性的时间复杂度（遍历几次数组）就能获得答案。
于是在经过几分钟思考后，我给出了一个错误的 动态规划 的思路。
面试官进一步提示我：这道题可以用很简单的方法解题，不用什么高深的算法。
于是我调整了一下思路继续思考问题，根据基本的几种情况进行了推导。
1、无负数情况下，取出最小值即可。
2、有负数情况下，根据负数的计数偶数个数来判断是取出，负数绝对值最小值，还是非负数绝对值最小值。
根据这个推断我们只需要一次遍历，记录负数个数，同时记录负数、非负数绝对值最小者。
于是我将思路讲给面试官，他笑了笑说，这个思路是对的，但是不能给我满分，要我再好好想一下，检查一下。
我知道，应该是有一些边界值还没有处理好，但是看了几分钟，还是没有找出问题。（人在紧张的情况下，思路会不太清晰）
于是，面试官指出了我面试中存在的问题，纯负数情况下，奇数个负数，应该排除绝对值奇数个，对于 0 这个边界值，也没有考虑到。一共应该是有 12 个分支，而我的代码只考虑了其中的 3、4 个（文章后面会画图解释）。
面试官进一步指导：在实际的代码开发中，可能并不会用太多高深的算法，但是像这道题一样的简单问题却很常见，我们需要考虑代码的健壮性，上线的代码仅考虑到 90% 的情况是错误的。
问题复盘
为什么是 12 个分支？
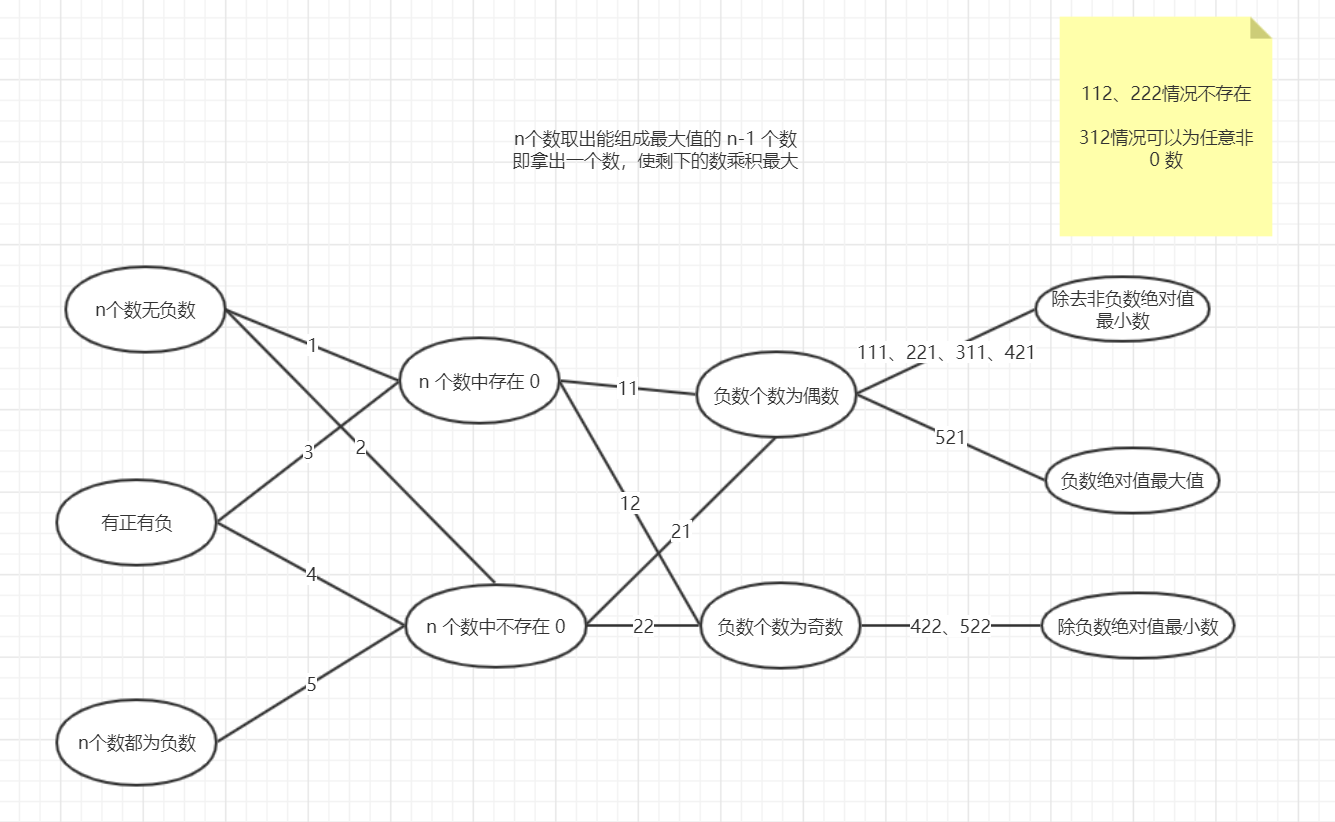
三个初始分支 n 个数都为非负数、n 个数有正有负、n 个数都为负数，以及 n 个数中是否存在 0，负数个数的奇偶个数 推导 332 = 12 个分支（0个负数视作偶数个，去除 2 个不存在情况，还剩 10 种需要考虑的情况）
实际可能出现的答案有三种：
1、无负数、有正有负且负数个数为偶数时，去除非负数绝对值最小者。
2、n 个数都为负数且负数个数个数为偶数时，去除负数绝对值最大者。
3、负数个数为奇数时，取负数绝对值最小者。（有正有负且存在 0，负数个数为奇数个可以去除任意非 0 数）
转换为实际代码：
/*
找出去除后集合乘积能达到最大的那个数
*/
int findMaxProductNum(int[] nums) {
int minMinus = Integer.MIN_VALUE, maxMinus = 0, minNum = Integer.MAX_VALUE, count = 0;
boolean hasZero = false;
// 一次遍历，统计负数个数，并判断 0 是否存在，更新负数/非负数 最大/小 绝对值
for (int i = 0; i < nums.length; i++) {
if (nums[i] < 0) {
count++;
maxMinus = Math.min(maxMinus, nums[i]);
minMinus = Math.max(minMinus, nums[i]);
} else if (nums[i] == 0) {
hasZero = true;
minNum = 0;
} else {
minNum = nums[i] < minNum ? nums[i] : minNum;
}
}
if (count == 0||(count<nums.length&&(count&1)==0)) { // 无负数、有正有负且负数个数为偶数时
return minNum;
} else if (count==nums.length&&(count&1)==0) { // n 个数都为负数且负数个数个数为偶数时
return maxMinus;
} else { // 负数个数为奇数时
return minMinus;
}
}
这道题的目的是什么？
考察一个求职者代码的健壮性，即能不能考虑全面，将问题的每个分支处理好。（可以先分解出输入的边界值，根据不同组合的分支推导结果。）
总结
1、 面试过程中，不要急于解题，要 和面试官确认好问题的边界。如果未明确，代码的健壮性就很有可能出现问题。
2、出错不要怕，好的面试官会引导你解题，注意提出问题后面试官给出的提示，这都是解题的方向。
3、几轮的面试是很累的，前一天做好休息，面试过程中 不要太紧张，会影响发挥，喝喝水调整下呼吸，放松下自己。
发表于 2019-11-3 18:02
|
发表于 2019-11-3 20:24
