好友
阅读权限10
听众
最后登录1970-1-1
|
极客先生
发表于 2020-2-16 18:38
以下所有程序的运行环境均为Code::Block，代码在不同编译器下运行，结果可能会有有所不同如，以下定义变量的位置并非全在程序开头，在VC上，可能会报错。改正方法：将程序里定义变量的语句放在程序的开头即可。
************************************************************************************************************************************************************************************************
话不多说，直接进入正题：一）：直接插入排序（插入排序有多种类型，这次讲平时应用最多的）
代码实现如下：（以正序输出为例，倒序输出，仅需对代码进行适当修改即可）
| 1234567891011121314151617181920212223242526272829303132333435363738 | #include<bits/stdc++.h>#include<algorithm>using namespace std; int a[100055]; int main(){ int n,i; cin>>n; for(i=1;i<=n;i++) { cin>>a; } int head; head = 2; while(head<=n) { i = head; while(i>=2&&a<a[i-1]) { if(a<a[i-1])//判断是否进行交换 { swap(a ,a[i-1]);//调用swap函数 i--; } } head++;//起索引作用，是循环的范围加1 } for(i=1;i<=n;i++) { cout<<a; } return 0;} |
上述代码的运行结果为：
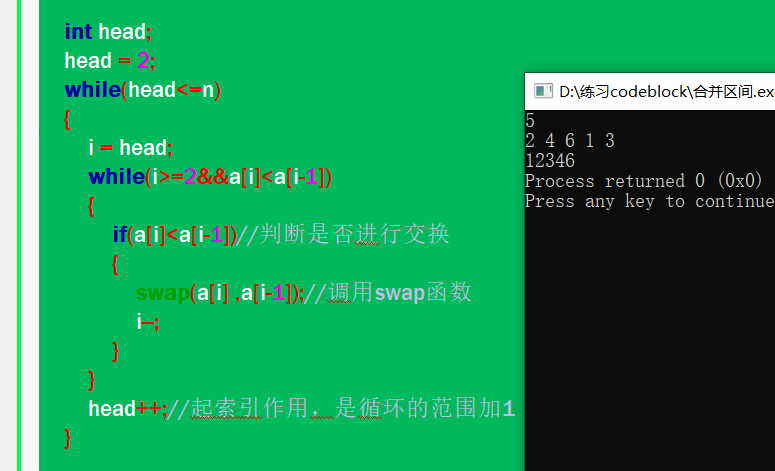
首先，我们来理一下上述代码的思想，上述代码实际上就是，每次while循环依次比较a[2]与a[1] ; a[3]与a[2] 、a[2]与a[1] ; a[4]与a[3]、a[3]与a[2]、a[2]与a[1] ; ………大小，直到遍历完数组所有的元素，也就完成了排序。
我们可以把上述代码总结成一种模型，即，上述代码可以对任意一组数据的任意一段连续数据进行排序（仅需改变上述代码的初始化条件以及循环结束条件即可实现），而这一思想的典型应用就是 “滚动的榜单”问题。
当然，上述代码也可以用for循环实现，但个人认为，用while循环，更能体现其思想本质，尤其是通过变量head，体现比较范围的变换。且在实际应用时，个人感觉，用while循环实现更加方便。二）：冒泡排序
代码如下（以正序输出为例）
| 12345678910111213141516171819202122232425262728293031323334 | #include<bits/stdc++.h>#include<algorithm>using namespace std; int a[55]; int main(){ int n,i; cin>>n; for(i=1;i<=n;i++) { cin>>a; } int head = 1; while(head<=n) { for(i=head+1;i<=n;i++) { if(a<a[head]) { swap(a ,a[head]); } } head++; } for(i=1;i<=n;i++) { cout<<a; } return 0;} |
上述代码的运行结果为：
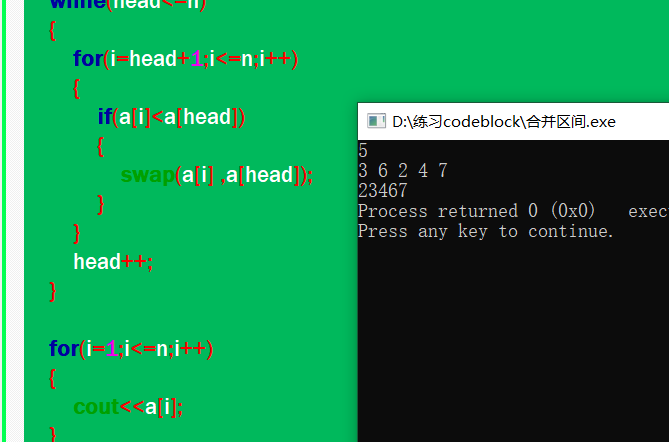
上述代码的思想是：首先，用数组的第一个元素与剩下的元素比较，并将最小的元素调到第一位；然后，用数组的第二个元素与剩下的元素比较，并将最小的元素调到第二位；以此类推，当head等于n时，就完成了排序。
上述算法，对于不搞竞赛的同学来说，应该是最常用的排序方法了。
上述代码同样可以用for循环实现。
三）：快速排序
具体代码如下（以升序形式输出）
| 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152 | #include<iostream>#include<algorithm>using namespace std; void quicksort(int l ,int r); int a[100055]; int main(){ int n,i; cin>>n; for(i=1;i<=n;i++) { cin>>a; } quicksort(1 ,n); for(i=1;i<=n;i++) { cout<<a<<" "; } cout<<endl; return 0;} void quicksort(int l ,int r){ int i,j,m,mid; i = l; j = r;<br> mid = (l+r)/2; m = a[mid];//将数组分成两部分 while(i<=j) {<br>/***********************************************/<br>//注意，这里while里面的判断条件为什么不带上 “=”？<br>//是为了防止当出现数组中出现一段相等的数字是，该循环变为死循环。如下面举出的例子。 while(a<m) i++; while(a[j]>m) j--;<br>/***********************************************/ if(i<=j) { swap(a ,a[j]); i++; j--; } } if(j-l>=1)//停止调用函数本身的判断条件 quicksort(l ,j);//通过调用函数自身，对分开的两部分，分别进行排序<br> //同时，由于i,j经过while循环，均越过了中值mid,故，新范围是（l ,j），下面的（i，r）同理。 if(r-i>=1)//停止调用函数本身的判断条件 quicksort(i ,r);//通过调用函数自身，对分开的两部分，分别进行排序} |
上述代码运行结果为：
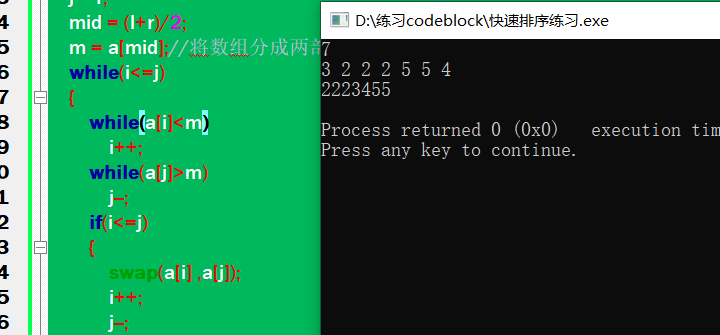
但当将while循环中的判断条件带上等号是，就会出现漏洞，可能使程序变为死循环，如：
file:///C:/Users/行之/AppData/Local/YNote/data/qq4AFEB2214132CC6DAB6F8DFBD8F630C0/17d75d4078b74f76992aa994e6059580/clipboard.png
file:///C:/Users/行之/AppData/Local/YNote/data/qq4AFEB2214132CC6DAB6F8DFBD8F630C0/17d75d4078b74f76992aa994e6059580/clipboard.png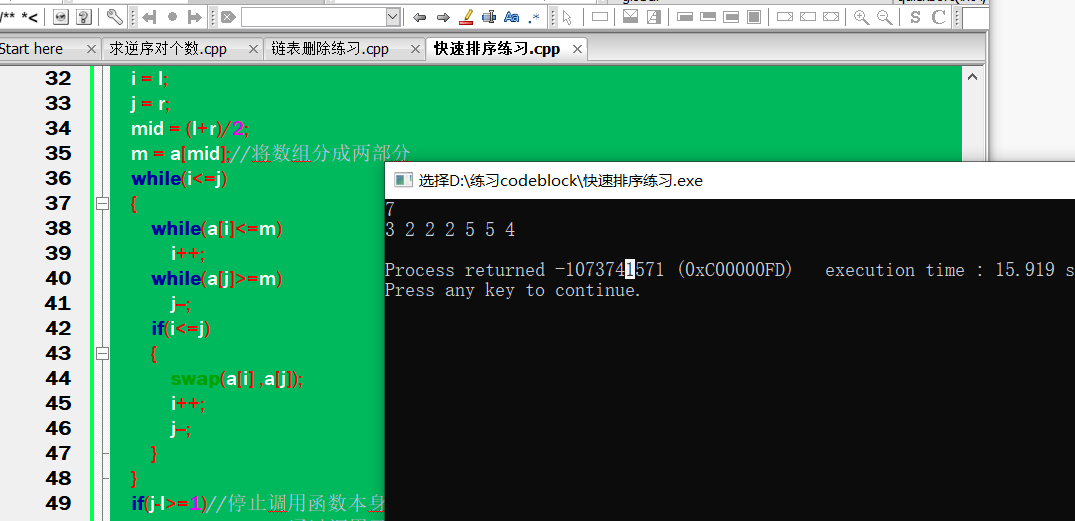
上述代码实际上体现了二分的思想：首先随机在数组中选一个数，将一个数组分成随机分成两部分（这里我就用区间的中间位置对应的值，实际上，可以用rand函数随机生成一个位置，这样其实更加合理），分别在左，右取大于或等于、小于或等于a[mid]的数，进行交换，直到i,j越过mid值时，一次循环结束。这样不断地进行循环，最终即可以实现排序。
快速排序的精髓就在于灵活应用二分的思想，这也正是其运行效率高的原因之一。
四）：归并排序
代码如下：（以升序为例）
#include<bits/stdc++.h>
using namespace std;
#define N 100055
void mergesort(int l, int r);
int a[N];
int larray[N],rarray[N],rn,ln,lposition,rposition;//larray[N],rarray[N]用于存储拆分得到的两个数组;
//ln ,rn 用于记录被分成的左右数组分别包含的元素的个数;
//lposition ,rposition 用于记录数组的下表所在的位置
int main()
{
int n,i;
cin>>n;
for(i=1;i<=n;i++)
cin>>a;
mergesort(1,n);
for(i=1;i<=n;i++)
{
cout<<a<<" ";
}
cout<<endl;
return 0;
}
void mergesort(int l,int r)
{
int i;
int mid=(l+r)/2;
//将数组分为两部分
if(l<mid)
mergesort(l,mid);//反复调用函数本身，实现排序
if(mid+1<r)
mergesort(mid+1,r);//反复调用函数本身，实现排序
ln=rn=0;
for(i=l;i<=mid;i++)
larray[++ln]=a;
for(i=mid+1;i<=r;i++)
rarray[++rn]=a;
lposition=rposition=1;
for(i=l;i<=r;i++)
{
//******************************************************************************/
//这部分用于解决数组中最后一个元素归属问题（因为对于数组的追后一个元素，已经没有其他元素来和他进行大小比较了，那么，也就不能利用下面的语句，通过比较两个数组大小为其中的元素分配位置。这时，
//必须单独设计语句，为最后的一个元素分配位置，也就有了下面的这两个语句）
if(lposition>ln)
a=rarray[rposition++];//lposition>ln的意思是，当前数组下标的位置已经超出了数组的有效长度，下同。
else if(rposition>rn)
a=larray[lposition++];
//*****************************************************************************/
else if(larray[lposition]<=rarray[rposition])//这两句是为数组中的元素分配位置，分配原则是数值小的先分配位置，下同。
a=larray[lposition++];
else
a=rarray[rposition++];
}
}
上述代码运行结果为：
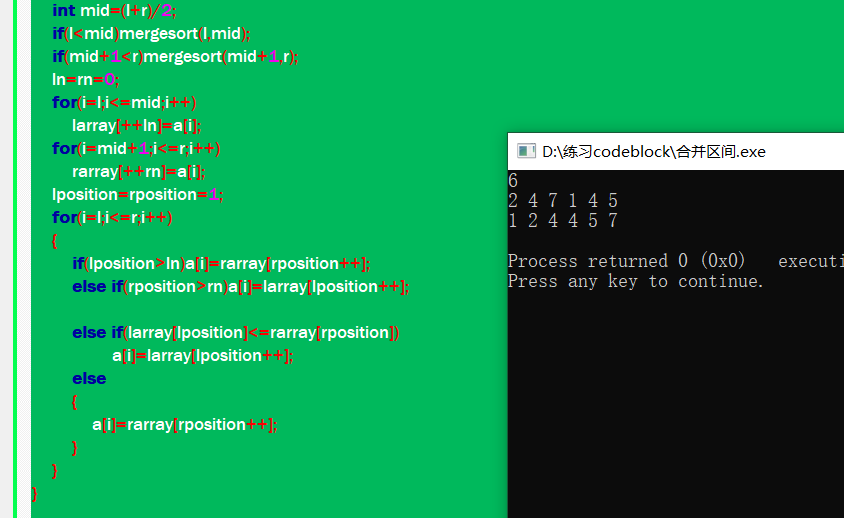
上述代码的核心思想是：先将数组利用二分思想多次进行二等分，然后在从得到的各个小份数组出发，两两遵循在合并的同时按从小到大排序，最终，即可实现排序。
具体图片如下：（下图摘自百度百科 ，链接：https://baike.baidu.com/pic/归并排序/1639015/0/c8177f3e6709c93d673b9ed49d3df8dcd00054c3
fr=lemma&ct=single#aid=0&pic=c8177f3e6709c93d673b9ed49d3df8dcd00054c3）
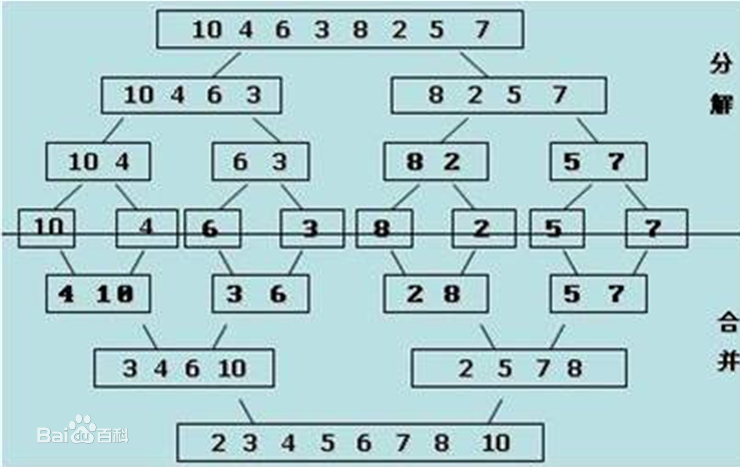
归并排序在上述几种排序方式中应该是最复杂的排序方式了，但其高效的运行效率，以及其包含的重要思想使得作为一个合格的程序员，或者是搞算法竞赛的同学必须掌握。
到目前为止，个人感觉，对上述归并排序算法的思想的应用最到位的当属经典的 “ 逆序数的对数” 问题。
五）二分法查找
除了介绍上述四种常用的排序方法外，我还想补充一下关于二分法查找的一下东西。（将一个数加入到一组数里面后，找出其在这组数里的位置）
先看代码实现：（以正序输入为例）
#include<iostream>
using namespace std;
const int maxint = 1000000000;
int main()
{
int a[100055];
int n,m;
cin>>n>>m;
int i;
for(i=1;i<=n;i++)
{
cin>>a;
}
a[0] = -maxint;
a[n+1] = maxint;//这个语句的作用就是为了防止因输入的数大于已知数据的最大值而造成程序不稳定
int l,r,mid,mark;
l = 0,r=n+1;
while(l<=r)
{
mid = (l+r)/2;
if(a[mid]>=m)
{
mark = mid;
r = mid-1;
}
else
{
l = mid+1;
}
}
cout<<mark<<endl;
return 0;
}
以上代码运行结果为：
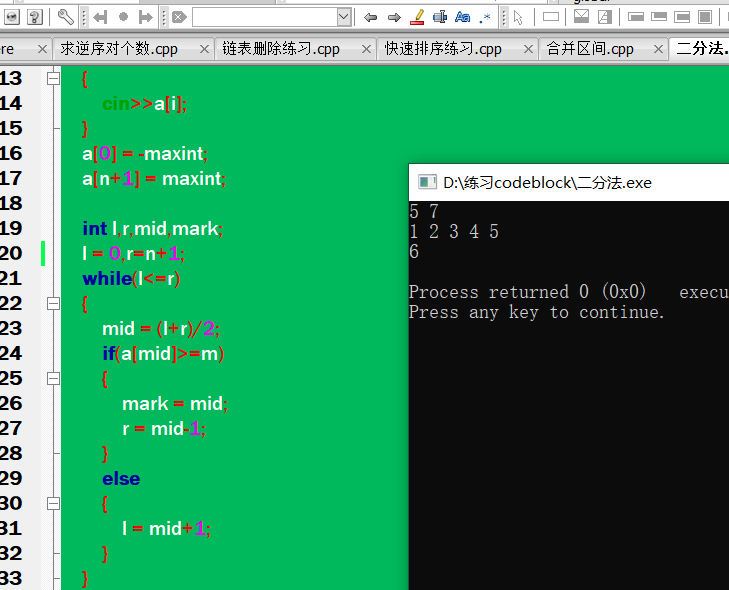
若没有上述语句，会：
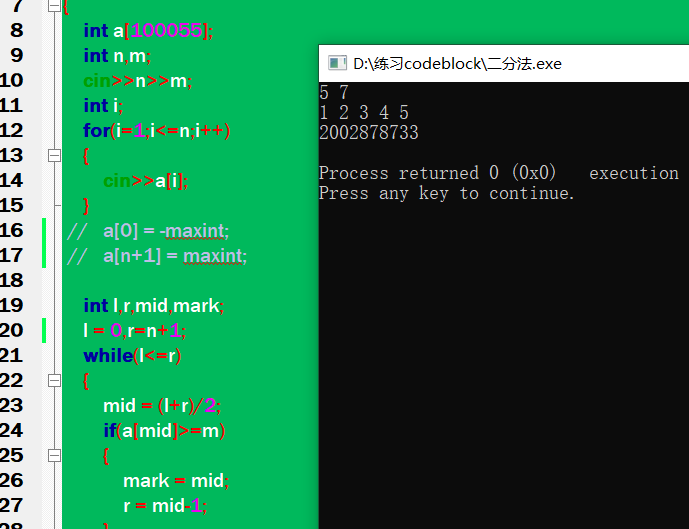
结果是乱码！！！
所以，我们在设计二分法的时候，一定要考虑当输入的值大于已知的最大值这种情况，当然，解决这个问题的方法不止上面一种，就不一一罗列了。
希望以上内容能对各位有所帮组！！！
*************************************************************************************************************************************************************************************************************************
再强调一次，以上代码均为 通过各种途径学习+自己的理解 所得，如若侵权，请告知，核实之后，必立即删除！！！
同时本人为大一菜鸟，上面的样例均为自主设置的，如若有误，还请告知，必立即改正。
本人写此文章主要目的是对知识点整理，但限于个人水平，如上述表述内容有些许错误，或不到位的地方，请各位大佬告知，在下必立刻更改！！！
欢迎大佬们评论，留言。
最后，码字不易，要是感觉还行的话，求求大佬们点个赞吧。 |
免费评分
-
查看全部评分
|
发帖前要善用【论坛搜索】功能，那里可能会有你要找的答案或者已经有人发布过相同内容了，请勿重复发帖。 |
|
|
|
|
|
|
|
发表于 2020-2-16 18:42
发表于 2020-2-16 21:37
