霍夫曼树
1、霍夫曼树的基本介绍
- 给定 n个权值作为 n个叶子结点，构造一棵二叉树，若该树的带权路径长度(wpl)达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)
- 哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近
2、霍夫曼树中的重要概念
路径：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。
路径长度：若规定根结点的层数为1，则从根结点到第L层结点的路径长度为 L-1 (例:第三层到根节点的长度为2)
结点的权：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权(一般是这个结点的值)
结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积（W×L）
树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和（W1×L1+W2×L2…），记为WPL(weighted pathlength) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。WPL最小的就是霍夫曼树。
3、创建思路
- 从小到大进行排序, 将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树（将数组中的数据，从小到大排序）
- 取出根节点权值最小的两颗二叉树（取值最小的两个数，也就是排序后，最前面的两个数）
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和（将这两个数作为树的子节点，本身的值为这两个数的和）
- 再将这颗新的二叉树，以根节点的权值大小 再次排序，不断重复 1-2-3-4 的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
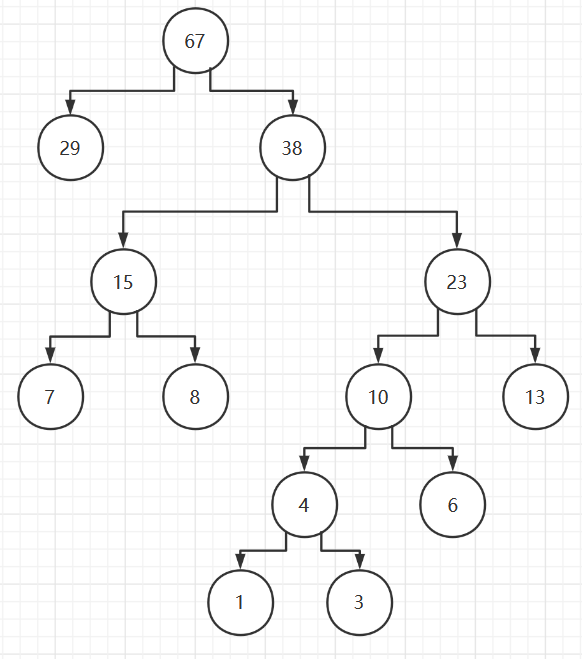
PS：对比的时候，新构建的树，和数组中的数做比较，若新的树的值比数组中的数小，则直接将这两个数作为树的子节点，构成新树。弱新的树值比数组中的数大，则取数组中两个数，以这两个数作为树的子节点，构成一颗新的树，再把这棵树，和前面的那颗树结合，构成新的树。（1,3,6,7,8，13,29）
4、霍夫曼编码
4.1、霍夫曼编码基本介绍
- 赫夫曼编码也翻译为哈夫曼编码(HuffmanCoding)，又称霍夫曼编码，是一种编码方式,属于一种程序算法
- 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%～90%之间
- 赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，称之为最佳编码
4.2、步骤介绍
1)要传输的字符串：i like like like java do you like a java
2)d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 //各个字符对应的个数
3)按照上面字符出现的次数构建一颗赫夫曼树,次数作为权值步骤：
构成赫夫曼树的步骤：
- 从小到大进行排序,将每一个数据，每个数据都是一个节点，每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树,该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树，以根节点的权值大小再次排序，不断重复1-2-3-4的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
4）根据赫夫曼树，给各个字符,规定编码(前缀编码)，向左的路径为0向右的路径为1，编码如下：o:1000u:10010d:100110y:100111i:101a:110k:1110e:1111j:0000v:0001l:001:01
5)无损压缩结果为：1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
通过赫夫曼编码处理长度为133
6）长度为：133说明:原来长度是359,压缩了(359-133)/359=62.9%，此编码满足前缀编码,即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性赫夫曼编码是无损处理方案
PS：赫夫曼树根据排序方法不同，也可能不太一样，这样对应的赫夫曼编码也不完全一样，但是wpl是一样的，都是最小的,最后生成的赫夫曼编码的长度是一样
发表于 2021-3-30 11:13
