【算法】位运算符基础之某CTF赛题使用Python与易语言纯算法还原

OVVO · 发表于 2022-10-7 22:22

本帖最后由 OVVO 于 2022-10-7 22:30 编辑

什么是位运算？

程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。比如，and运算本来是一个逻辑运算符，但整数与整数之间也可以进行and运算。举个例子，6的二进制是110，11的二进制是1011，那么6 and 11的结果就是2，它是二进制对应位进行逻辑运算的结果（0表示False，1表示True，空位都当0处理）。

位运算(Bit Manipulation,也叫位操作)说穿了，就是直接对整数在内存中的二进制位进行操作。

含义	Pascal语言	C/C++语言	Java	Php
按位与	a and b	a & b	a & b	a & b
按位或	a or b	a \| b	a \| b	a \| b
按位异或	a xor b	a ^ b	a ^ b	a ^ b
按位取反	not a	~a	~a	~a
左移	a shl b	a <<b	a <<b	a << b
带符号右移	a shr b	a >> b	a >> b	a >> b
无符号右移	/	/	a>>> b	/

简单的说

含义	运算符
与	&
或	\|
异或	^
取反	~
左移	<<
右移	>>
无符号右移	>>>

数的存储

计算机中数是以二进制补码进行存储的，正数的原码、反码、补码都是一样，负数的补码是原码的反码再加1，这样可以减法运算可以使用加法器实现，符号位也参与运算（二进制的最高位为符号位0为正，1为负，以8位来算，最高位为符号位，其余7位表示数值），取反码与符号位无关。

int类型的数占用4字节（32位）。5转换成二进制是101，不满32位会在前面填充0。那么5在计算机中表示为：00000000 00000000 00000000 00000101

原码，反码与补码

原码：一个整数，按照绝对值大小转换成的二进制数；
反码：将二进制数按位取反【1变0，0变1】；
补码：反码加 1；

负数的二进制

如十进制【-5】

        原码: 00000000 00000000 00000000 00000101
        反码：11111111 11111111 11111111 11111010
补码(反码加一)：11111111 11111111 11111111 11111011

所以 -5 的二进制是 11111111 11111111 11111111 11111011，转换为十六进制：0xFFFFFFFB。

二进制求整

如补码是：11111111 11111111 11111111 11110010

        补码: 11111111 11111111 11111111 11110010
反码(补码减一)：11111111 11111111 11111111 11110001
按位取反，原码：00000000 00000000 00000000 00001110

原码00000000 00000000 00000000 00001110即14, 然后取反就是 -14。

<<左移

运算规则：按二进制形式把所有的数字向左移动对应的位数，高位移出(舍弃)，低位的空位补零。
语法格式：需要移位的数字 << 移位的次数。
数学意义：如果是10进制向左移动一位相当于乘10倍，移两位乘10的2次方倍，所以在数字没有溢出的前提下，对于正数和负数，二进制左移n位就相当于乘以2的n次方。

/** 3 << 2 **/
3转化为二进制: 00000011
    移动补位：00001100
 转化为十进制：12

3 2 ^ 2 = 3 4 = 12

易语言版

调试输出 (左移 (3, 2))

为什么没有无符号左移<<<?
因为左位移是填补右边空出的位，符号位不影响它的值。

>>带符号右移

运算规则：按二进制形式把所有的数字向右移动对应的位数，低位移出(舍弃)，高位的空位补符号位，即正数补零，负数补1。【补的位数全部是符号位】
语法格式：需要移位的数字 >> 移位的次数
数学意义：右移一位相当于除2，右移n位相当于除以2的n次方。商若为小数，取整即可。

/** 11 >> 2 **/     
11转化为二进制: 0000 1011
     移动补位：0000 0010
  转化为十进制：2

11 / 2^2 = 11 / 4 = 2

易语言版

调试输出 (右移 (11, 2))

负数右移

例如： -100 >> 4【-100带符号右移4位】

        -100原码：00000000 00000000 00000000 01100100
        -100反码：11111111 11111111 11111111 10011011
        -100补码：11111111 11111111 11111111 10011100
右移4位，在高位补1：11111111 11111111 11111111 11111001

补码形式的移位完成后，结果不是移位后的结果，要根据补码写出原码才是最后的结果。

    减一：11111111 11111111 11111111 11111000
 按位取反：00000000 00000000 00000000 00000111
添加符号位：10000000 00000000 00000000 00000111
     结果：-7

易语言版

调试输出 (右移 (-100, 4))

>>>无符号右移

\>\>\>运算符执行无符号右移位运算，它把无符号的 32 位整数所有数位整体右移。最左侧空位不再用符号位的值来填充，而是用 0 来填充。

// 对于无符号数或正数，无符号右移与有符号右移运算结果相同。
console.log(1000 >> 8);  // 3
console.log(1000 >>> 8);  // 3

console.log(-1000 >> 8);  // -4
console.log(-1000 >>> 8);  // 16777212

~非

运算规则：操作数被转换为32位二进制表示（0和1）。超过32位的数字将丢弃其最高有效位。
语法格式： ~ 操作数。
数学意义：任何数 x 的运算结果都是-(x + 1)。~-5运算结果为`4；

/** ~ 5 **/
5转化为二进制: 00000000 00000000 00000000 00000101
    位数取反: 11111111 11111111 11111111 11111010 【补码】
       反码：11111111 11111111 11111111 11111001
       原码：00000000 00000000 00000000 00000110
  添加符号位：10000000 00000000 00000000 00000110
 转化为十进制: -6

const a = 5;
console.log(~a); // -6

易语言版

调试输出 (位取反 (5))

& 与

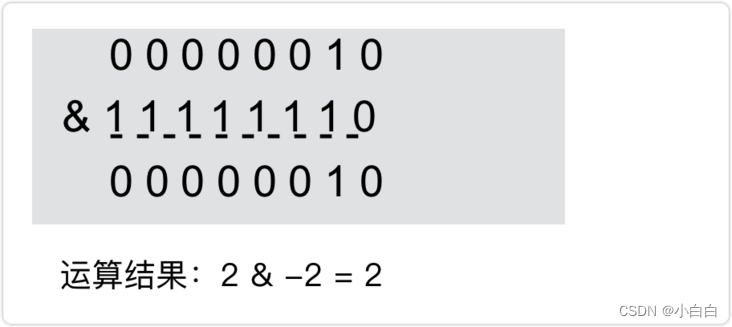
运算规则：第一个操作数的第n位与第二个操作数的第n位对比，如果都是1，那么第n位的结果为1，否则为0；同真为真，一假为假。

5转换为二进制：00000000 00000000 00000000 00000101
3转换为二进制：00000000 00000000 00000000 00000011
 5 & 3 结果：00000000 00000000 00000000 00000001

5 & 3 结果：00000000 00000000 00000000 00000001，转化为二进制是1；

在这里插入图片描述

易语言版

调试输出 (位与 (5, 3))

|或

运算规则：第一个操作数的第n位与第二个操作数的第n位对比，只要有一个是1，那么第n位的结果为1，否则为0；一真为真，同假为假

5转换为二进制：00000000 00000000 00000000 00000101
3转换为二进制：00000000 00000000 00000000 00000011
  5 | 3 结果：00000000 00000000 00000000 00000111

5 | 3 结果：00000000 00000000 00000000 00000111，转化为二进制是7；

在这里插入图片描述

易语言版

调试输出 (位或 (5, 3))

^异或

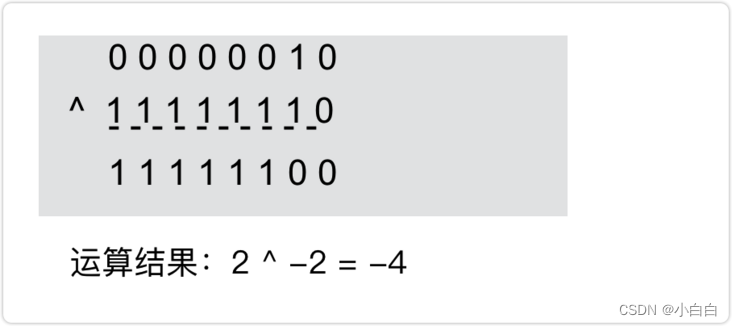
运算规则：第一个操作数的第n位与第二个操作数的第n位对比，如果相反那么第n位结果的为1，否则为0；同为假，异为真

5转换为二进制：00000000 00000000 00000000 00000101
3转换为二进制：00000000 00000000 00000000 00000011
  5 ^ 3 结果：00000000 00000000 00000000 00000110

5 ^ 3 结果：00000000 00000000 00000000 00000110，转化为二进制是6；

在这里插入图片描述

易语言版

调试输出 (位异或 (5, 3))

位运算小技巧，判断奇偶

正常判断奇数偶数的时候我们会这样写：

if( n % 2 == 1)
    // n 是个奇数
}

使用位运算可以这么写：

if(n & 1 == 1){
    // n 是个奇数。
}

其核心就是判断二进制的最后一位是否为1，如果为1那么结果加上2^0=1一定是个奇数，否则就是个偶数。

a & 1 == 0; // 偶数
a & 1 == 1; // 奇数

位运算小技巧，交换两个数的值

对于传统的交换两个数，我们需要使用一个变量来辅助完成操作，可能会是这样：

int team = a;
a = b;
b = team;

但是使用位运算可以不需要借助额外空间完成数值交换：

a=a^b;//a=a^b
b=a^b;//b=(a^b)^b=a^0=a
a=a^b;//a=(a^b)^(a^b^b)=0^b=0

异或运算有如下特性：a ^ b ^ a = b; a ^ b ^ b = a

x ^= y;
y ^= x;
x ^= y;

图解：负数的移位运算符

在这里插入图片描述

CTF算法题目

来源网络：BUUCTF Reverse/[网鼎杯 2020 青龙组]jocker
在这里插入图片描述
查壳：32位无壳程序，直接拖ida

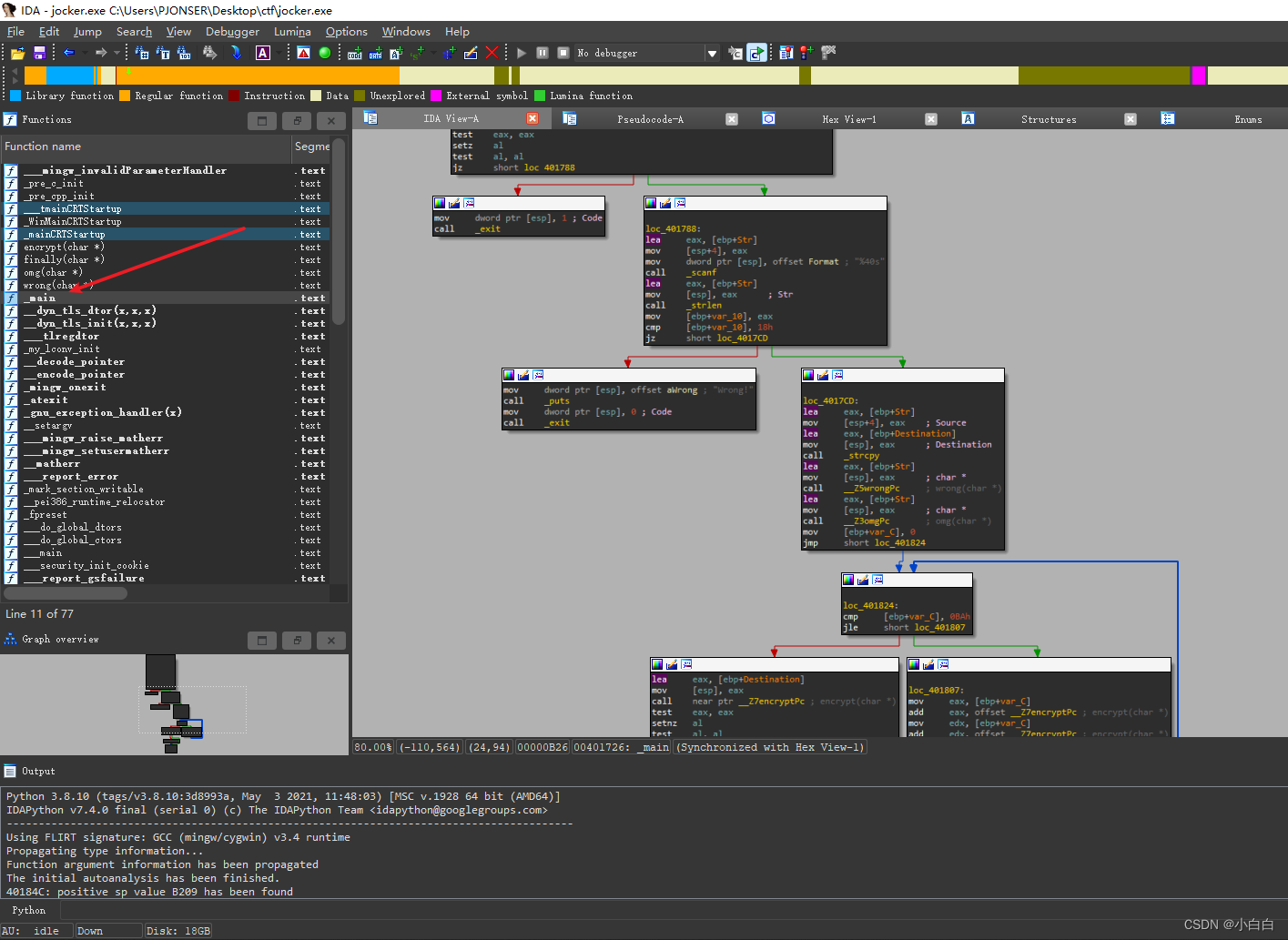
在这里插入图片描述

首先shift+f12搜索字符串，但是除了main函数中的一句请输入flag提示之外在没有什么有用的。

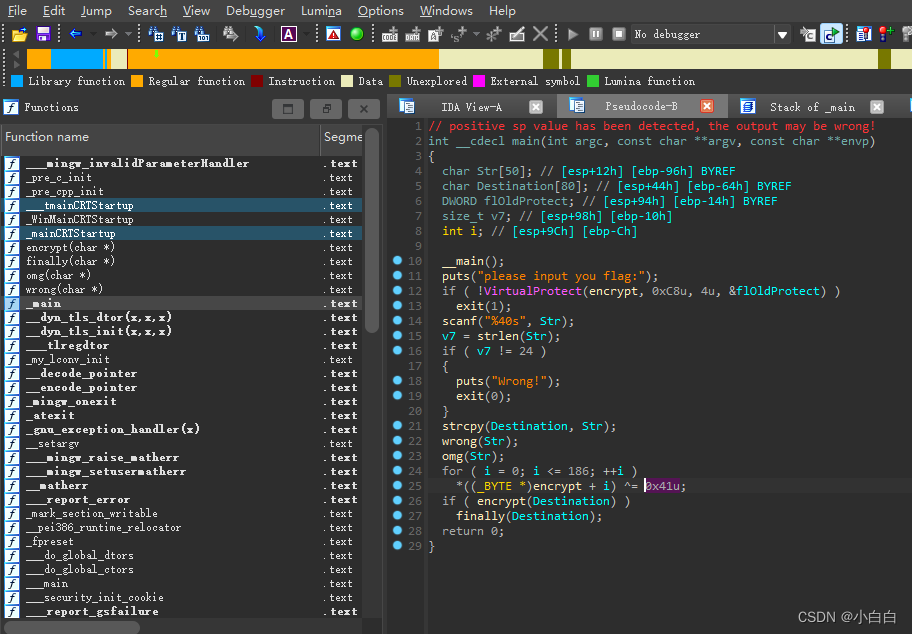
main函数

// positive sp value has been detected, the output may be wrong!
int __cdecl main(int argc, const char **argv, const char **envp)
{
  char Str[50]; // [esp+12h] [ebp-96h] BYREF
  char Destination[80]; // [esp+44h] [ebp-64h] BYREF
  DWORD flOldProtect; // [esp+94h] [ebp-14h] BYREF
  size_t v7; // [esp+98h] [ebp-10h]
  int i; // [esp+9Ch] [ebp-Ch]

  __main();
  puts("please input you flag:");
  if ( !VirtualProtect(encrypt, 0xC8u, 4u, &flOldProtect) )
    exit(1);
  scanf("%40s", Str);
  v7 = strlen(Str);
  if ( v7 != 24 )
  {
    puts("Wrong!");
    exit(0);
  }
  strcpy(Destination, Str);
  wrong(Str);
  omg(Str);
  for ( i = 0; i <= 186; ++i )
    *((_BYTE *)encrypt + i) ^= 0x41u;
  if ( encrypt(Destination) )
    finally(Destination);
  return 0;
}

可以看到第一个条件是flag长度要为24

然后将str先复制到Destination这里，再调用wrong函数对str进行修改。

wrong函数

char *__cdecl wrong(char *a1)
{
  char *result; // eax
  int i; // [esp+Ch] [ebp-4h]

  for ( i = 0; i <= 23; ++i )
  {
    result = &a1[i];
    if ( (i & 1) != 0 )
      a1[i] -= i;
    else
      a1[i] ^= i;
  }
  return result;
}

在这里插入图片描述
可以看出wrong函数的功能是把a1里每个元素按照下标的奇偶进行相应的加密处理

然后来到omg函数
omg函数

int __cdecl omg(char *a1)
{
  int v2[24]; // [esp+18h] [ebp-80h] BYREF
  int i; // [esp+78h] [ebp-20h]
  int v4; // [esp+7Ch] [ebp-1Ch]

  v4 = 1;
  qmemcpy(v2, &unk_4030C0, sizeof(v2));
  for ( i = 0; i <= 23; ++i )
  {
    if ( a1[i] != v2[i] )
      v4 = 0;
  }
  if ( v4 == 1 )
    return puts("hahahaha_do_you_find_me?");
  else
    return puts("wrong ~~ But seems a little program");
}

查看unk_430C0部分
在这里插入图片描述
直接给出字符串了，破解一下吧(shift + E直接导出字符串)


key = 0x66,0x6B,0x63,0x64,0x7F,0x61,0x67,0x64,0x3B,0x56,0x6B,0x61,0x7B,0x26,0x3B,0x50,0x63,0x5F,0x4D,0x5A,0x71,0x0C,0x37,0x66
flag = ''
for i in range(24):
    if i % 2 == 1:
        flag += chr(key[i] + i)
    else:
        flag += chr(key[i] ^ i)
print(flag)
#结果：
#flag{fak3_alw35_sp_me!!}

假的flag

在omg后面还有一个循环，最后的一点应该是在这里的

循环中还有一个encrypt函数，但是无法打开
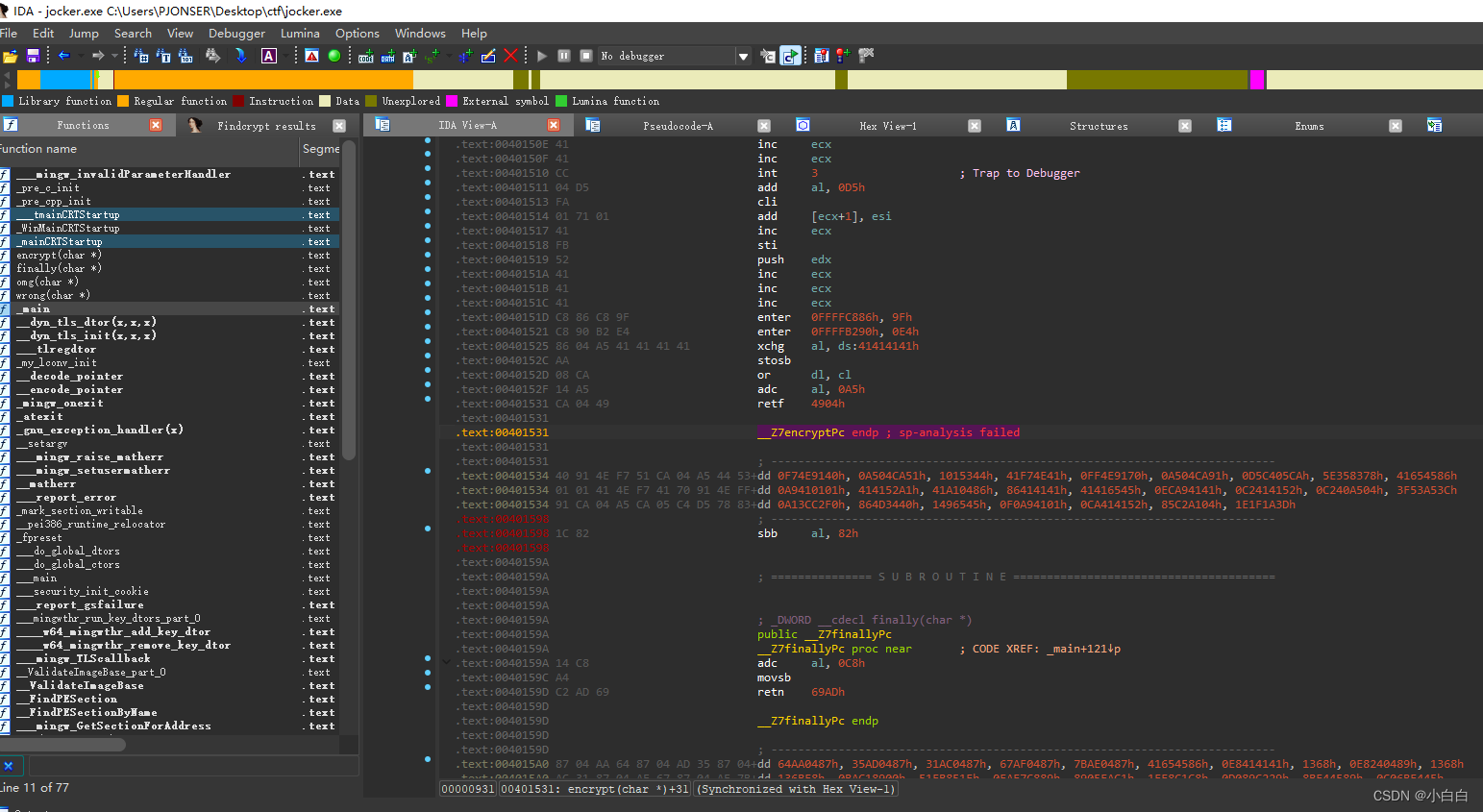
在这里插入图片描述

红色标注的下面那里像是一段乱码一样，导致无法反汇编出来结果吧，然后尝试找出调用了encrypt函数的地址，od动调一下，看看这个函数到底在干什么

在这里发现了encrypt函数和finally函数分别被调用

既然由前面的函数得到的flag是个假的，那最后正确的flag一定是通过这两个函数处理的，下一步就是分析encrypt函数

OD打开后在0x401833地址处下断点

在这里插入图片描述
然后F9运行至断点处，在应用中随意输入24位字符

然后F7步入
在这里插入图片描述
可以看到这里的函数是已经解密了，然后可以直接olldump脱壳，直接保存新的exe

然后再用ida打开它

encrypt函数

int __cdecl start(int a1)
{
  int v2[19]; // [esp+1Ch] [ebp-6Ch] BYREF
  int v3; // [esp+68h] [ebp-20h]
  int i; // [esp+6Ch] [ebp-1Ch]

  v3 = 1;
  qmemcpy(v2, &unk_403040, sizeof(v2));
  for ( i = 0; i <= 18; ++i )
  {
    if ( (char)(*(_BYTE *)(i + a1) ^ aHahahahaDoYouF[i]) != v2[i] )
    {
      puts("wrong ~");
      v3 = 0;
      exit(0);
    }
  }
  puts("come here");
  return v3;
}

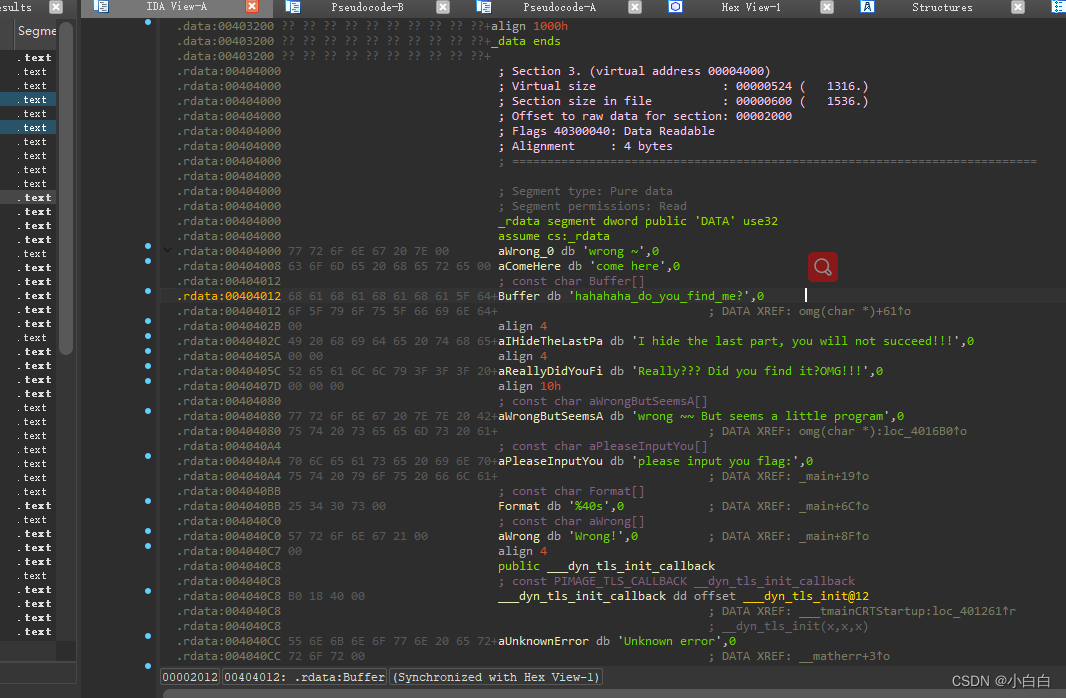
在这里插入图片描述
aHahahahaDoYouF中的字符串是hahahaha_do_you_find_me?

unk_403040中的字符通过shift + E 可以直接导出

然后写个脚本破解一下

写法一：

v2 = [14, 13, 9, 6, 19, 5, 88, 86, 62, 6, 12, 60, 31, 87, 20, 107, 87, 89, 13]
xor = 'hahahaha_do_you_find_me?'
flag = []
for i in range(0, 19):
    flag.append(v2[i] ^ ord(xor[i]))
for i in range(0, 19):
    print(chr(flag[i]), end = '')

写法二：

a = [14,13,9,6,19,5,88,86,62,6,12,60,31,87,20,107,87,89,13]
s = "hahahaha_do_you_find_me?"
flag = ""
for i in range(19):
    flag += chr(ord(s[i]) ^ a[i])
print(flag)

得到结果是

flag{d07abccf8a410c

flag明显少了一部分啊，但是它最后还有一个
finally函数

int __cdecl sub_40159A(int a1)
{
  unsigned int v1; // eax
  char v3[9]; // [esp+13h] [ebp-15h] BYREF
  int v4; // [esp+1Ch] [ebp-Ch]

  strcpy(v3, "%tp&:");
  v1 = time(0);
  srand(v1);
  v4 = rand() % 100;
  v3[6] = 0;
  *(_WORD *)&v3[7] = 0;
  if ( (v3[(unsigned __int8)v3[5]] != *(_BYTE *)((unsigned __int8)v3[5] + a1)) == v4 )
    return puts("Really??? Did you find it?OMG!!!");
  else
    return puts("I hide the last part, you will not succeed!!!");
}

这段代码具体是什么意思真的没搞明白，但是前面的加密算法是异或，所以尝试一下异或

得到的flag现在没有最后一位 }，那么剩下的字符串里肯定是最后一个字符异或一个数得到}

flag = []
v3 = [37, 116, 112, 38, 58]#既是‘%tp&:’
key = ord('}') ^ 58
for i in range(5):
    flag.append(chr(v3[i] ^ key))
print(''.join(flag))

最后得到

b37a}

最终拼接得到flag

flag{d07abccf8a410cb37a}

还原算法

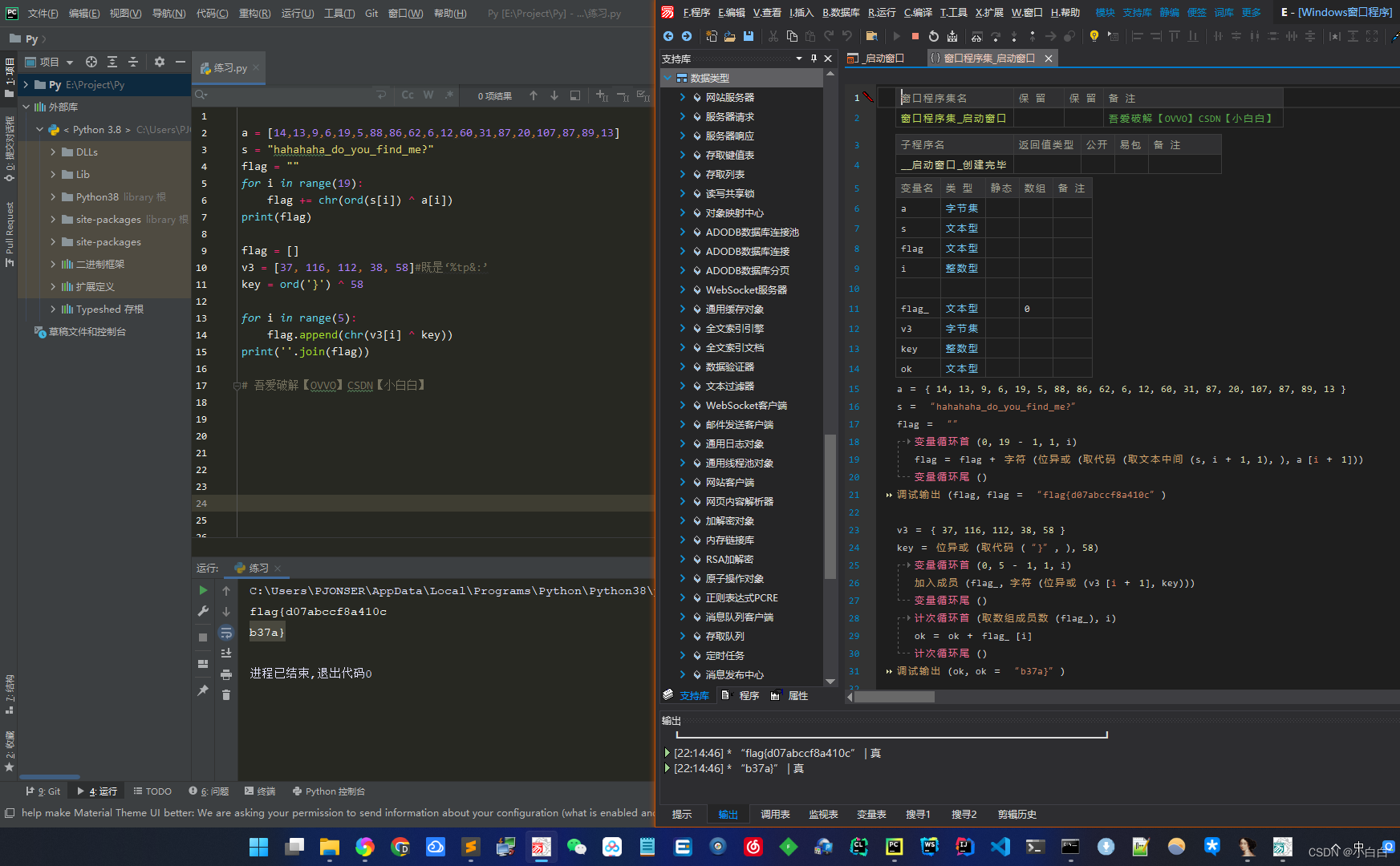
在这里插入图片描述
python版本


a = [14,13,9,6,19,5,88,86,62,6,12,60,31,87,20,107,87,89,13]
s = "hahahaha_do_you_find_me?"
flag = ""
for i in range(19):
    flag += chr(ord(s[i]) ^ a[i])
print(flag)

flag = []
v3 = [37, 116, 112, 38, 58]#既是‘%tp&:’
key = ord('}') ^ 58

for i in range(5):
    flag.append(chr(v3[i] ^ key))
print(''.join(flag))

易语言版本

.版本 2
.支持库 spec

.程序集 窗口程序集_启动窗口

.子程序 __启动窗口_创建完毕
.局部变量 a, 字节集
.局部变量 s, 文本型
.局部变量 flag, 文本型
.局部变量 i, 整数型
.局部变量 flag_, 文本型, , "0"
.局部变量 v3, 字节集
.局部变量 key, 整数型
.局部变量 ok, 文本型

a ＝ { 14, 13, 9, 6, 19, 5, 88, 86, 62, 6, 12, 60, 31, 87, 20, 107, 87, 89, 13 }
s ＝ “hahahaha_do_you_find_me?”
flag ＝ “”
.变量循环首 (0, 19 － 1, 1, i)
    flag ＝ flag ＋ 字符 (位异或 (取代码 (取文本中间 (s, i ＋ 1, 1), ), a [i ＋ 1]))
.变量循环尾 ()
调试输出 (flag, flag ＝ “flag{d07abccf8a410c”)

v3 ＝ { 37, 116, 112, 38, 58 }
key ＝ 位异或 (取代码 (“}”, ), 58)
.变量循环首 (0, 5 － 1, 1, i)
    加入成员 (flag_, 字符 (位异或 (v3 [i ＋ 1], key)))
.变量循环尾 ()
.计次循环首 (取数组成员数 (flag_), i)
    ok ＝ ok ＋ flag_ [i]
.计次循环尾 ()
调试输出 (ok, ok ＝ “b37a}”)

djlt · 发表于 2023-5-9 01:31

你好你的联系方式是多少我刚注册论坛无法向你发信息有点事找你一下。

djlt · 发表于 2023-5-9 01:30

你好你的联系方式是多少我刚注册论坛无法向你发信息有点事找你一下。

风雨3137 · 发表于 2022-10-8 08:59

牛啊，学习到了

GoogleHacking · 发表于 2022-10-8 09:48

没看懂，告绝很高大上的样子

ab123 · 发表于 2022-10-8 19:17

学习了，自己的脚本编写能力还有待加强

yiliber · 发表于 2022-10-9 11:19

感谢楼主的分享

2snfks29fais · 发表于 2022-10-9 12:58

感谢分享

luyao1 · 发表于 2022-10-9 18:10

谢谢分享

laiwanzhou · 发表于 2022-10-9 19:14

mark一下

善良的狼 · 发表于 2022-12-29 02:07

谢谢，学习了

Zupup · 发表于 2022-12-30 17:18

学到知识了

帐号		自动登录	找回密码
密码			注册[Register]

[原创] 【算法】位运算符基础之某CTF赛题使用Python与易语言纯算法还原

什么是位运算？

数的存储

原码，反码与补码

负数的二进制

二进制求整

<<左移

>>带符号右移

负数右移

>>>无符号右移

~非

& 与

|或

^异或

位运算小技巧，判断奇偶

位运算小技巧，交换两个数的值

图解：负数的移位运算符

CTF算法题目

还原算法

免费评分

免费评分