介绍
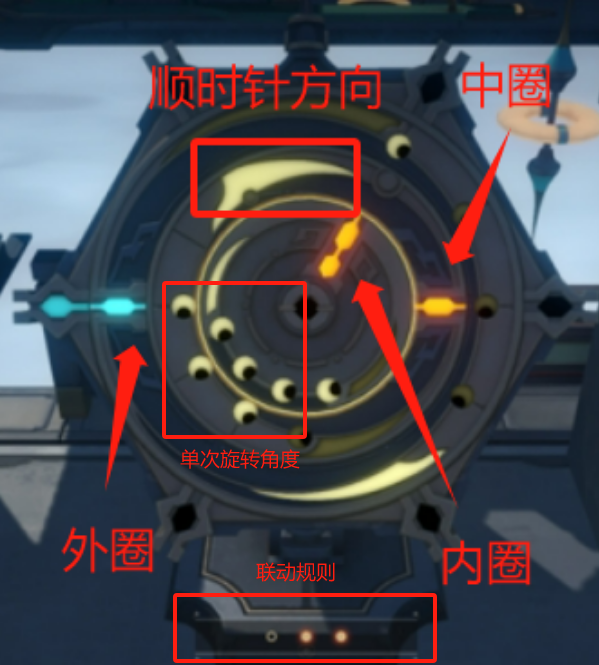
引航罗盘是游戏《星穹铁道》中的一个解密小游戏，由外圈、中圈、内圈三层同心圆组成，每个圆环分别具有：
- 指针一枚
- 初始角度
- 单次旋转角度，每亮一个点单次旋转多60度，共60、120、180、240四档
- 旋转方向，分为顺时针、逆时针
罗盘还具有三个联动规则，每个规则代表按一次，会有哪一层或哪两层圈同时转动（例如：规则1：内圈和外圈会同时转动；规则2：内圈和中圈会同时转动；规则3：外圈会单独转动）
最终目标：三个圈的指针全部指向左侧
罗盘示意图：
解题
设坐标系以罗盘中心为原点，假设罗盘按照规则1转动了x次，规则2转动了y次，规则3转动了z次后，外圈恰好第i次到达左侧目标角度，中圈恰好第j次到达目标，内圈恰好第k次到达目标
以角度为等式，可以列出一个3方程的6元1次方程组，显然是解不出来的：
外圈：a1*x+a2*y+a3*z=b1*i
中圈：a4*x+a5*y+a6*z=b2*j
内圈：a7*x+a8*y+a9*z=b3*k
对于计算机来说，可以用三重循环来模拟所有的i, j, k的情况（限定遍历的次数），将6元变成3元，从而能够使用克拉默法则进行求解
代码实现
无numpy，原生python实现
import copy
class Game:
def __init__(self) -> None:
self.direction = [-1, 1] # -1逆时针，1顺时针
self.rotate = [60, 120, 180, 240] # 共4档旋转
self.init = [0, 60, 120, 180, 240, 300] # 初始状态共6档
self.disk = [
{
"name": "内圈",
"direction": self.direction[0],
"rotate": self.rotate[0],
"init": self.init[0],
"angle": 0
},
{
"name": "中圈",
"direction": self.direction[0],
"rotate": self.rotate[0],
"init": self.init[0],
"angle": 0
},
{
"name": "外圈",
"direction": self.direction[0],
"rotate": self.rotate[0],
"init": self.init[0],
"angle": 0
},
]
self.coordination = [
[], # 两圈联动索引，写为列表格式，内圈0，中圈1，外圈2，无联动设置另一位为-1
[],
[]
]
print("==输入初始罗盘信息：==")
print("==内圈：==")
self.disk[0]["direction"] = self.direction[int(input("逆时针(0)/顺时针(1): "))]
self.disk[0]["rotate"] = self.rotate[int(input("旋转步长(输入亮着几颗星): ")) - 1]
self.disk[0]["init"] = self.init[int(input("初始角度(输入角度/60的值): "))]
print("==中圈：==")
self.disk[1]["direction"] = self.direction[int(input("逆时针(0)/顺时针(1): "))]
self.disk[1]["rotate"] = self.rotate[int(input("旋转步长(输入亮着几颗星): ")) - 1]
self.disk[1]["init"] = self.init[int(input("初始角度(输入角度/60的值): "))]
print("==外圈：==")
self.disk[2]["direction"] = self.direction[int(input("逆时针(0)/顺时针(1): "))]
self.disk[2]["rotate"] = self.rotate[int(input("旋转步长(输入亮着几颗星): ")) - 1]
self.disk[2]["init"] = self.init[int(input("初始角度(输入角度/60的值): "))]
print("==联动规则：==")
print("== 内/中/外 分别为 0/1/2 ; *单个旋转另一位写-1* ==")
self.coordination[0] = [int(input("联动1.1: ")), int(input("联动1.2: "))]
self.coordination[1] = [int(input("联动2.1: ")), int(input("联动2.2: "))]
self.coordination[2] = [int(input("联动3.1: ")), int(input("联动3.2: "))]
print("=====================================================================")
print(f'==内圈 -> 初始：{self.disk[0]["init"]} -> 旋转方向：{self.get_direction(self.disk[0]["direction"])} -> 步长：{self.disk[0]["rotate"]}')
print(f'==中圈 -> 初始：{self.disk[1]["init"]} -> 旋转方向：{self.get_direction(self.disk[1]["direction"])} -> 步长：{self.disk[1]["rotate"]}')
print(f'==外圈 -> 初始：{self.disk[2]["init"]} -> 旋转方向：{self.get_direction(self.disk[2]["direction"])} -> 步长：{self.disk[2]["rotate"]}')
print(f'==联动规则 -> 1.{self.get_rules(self.coordination[0])} -> 2.{self.get_rules(self.coordination[1])} -> 3.{self.get_rules(self.coordination[2])}')
print("=====================================================================")
@staticmethod
def get_direction(num: int) -> str:
return "逆时针" if num == -1 else "顺时针"
@staticmethod
def get_rules(rule: list) -> str:
def get_str(num: int) -> str:
if num == 0:
return "内圈"
elif num == 1:
return "中圈"
else:
return "外圈"
return f'{get_str(rule[0])}<+>{get_str(rule[1])}'
# 答案计算主程序
def cal(self) -> bool:
# 最终目标：三圈状态均为180
# x, y, z 三个变量，分别对应三个联动规则所需次数
# 内圈旋转次数：exist(self.coordination[0], 0) * x + exist(self.coordination[1], 0) * y + exist(self.coordination[2], 0) * z
# 中圈旋转次数：exist(self.coordination[0], 1) * x + exist(self.coordination[1], 1) * y + exist(self.coordination[2], 1) * z
# 外圈旋转次数：exist(self.coordination[0], 2) * x + exist(self.coordination[1], 2) * y + exist(self.coordination[2], 2) * z
# 内圈最终方程：
# exist(self.coordination[0], 0) * x + exist(self.coordination[1], 0) * y + exist(self.coordination[2], 0) * z = count(self.disk[0]["init"], self.disk[0]["direction"], self.disk[0]["rotate"])
# 中圈最终方程：
# exist(self.coordination[0], 1) * x + exist(self.coordination[1], 1) * y + exist(self.coordination[2], 1) * z = count(self.disk[1]["init"], self.disk[1]["direction"], self.disk[1]["rotate"])
# 外圈最终方程：
# exist(self.coordination[0], 2) * x + exist(self.coordination[1], 2) * y + exist(self.coordination[2], 2) * z = count(self.disk[2]["init"], self.disk[2]["direction"], self.disk[2]["rotate"])
# 用克拉默法则计算：
# 左侧系数矩阵
raw = [[self.exist(self.coordination[0], 0), self.exist(self.coordination[1], 0), self.exist(self.coordination[2], 0)],
[self.exist(self.coordination[0], 1), self.exist(self.coordination[1], 1), self.exist(self.coordination[2], 1)],
[self.exist(self.coordination[0], 2), self.exist(self.coordination[1], 2), self.exist(self.coordination[2], 2)]]
# 右侧系数矩阵
rep = [self.count(self.disk[0]["init"], self.disk[0]["direction"], self.disk[0]["rotate"]),
self.count(self.disk[1]["init"], self.disk[1]["direction"], self.disk[1]["rotate"]),
self.count(self.disk[2]["init"], self.disk[2]["direction"], self.disk[2]["rotate"])]
# 原行列式值
D = self.calculate(raw)
# 可能不止一次到达目的地，通过遍历的方式寻找答案
# 这是到达180度后继续旋转再次到达180度所需的次数
chg_1 = self.count(180 + self.disk[0]["rotate"], -1, self.disk[0]["rotate"]) + 1
chg_2 = self.count(180 + self.disk[1]["rotate"], -1, self.disk[1]["rotate"]) + 1
chg_3 = self.count(180 + self.disk[2]["rotate"], -1, self.disk[2]["rotate"]) + 1
# 遍历得到新的系数矩阵
num = 5 # 遍历层数
for i in range(num):
for j in range(num):
for k in range(num):
rep_temp = rep.copy()
rep_temp[0] = rep[0] + chg_1 * i
rep_temp[1] = rep[1] + chg_2 * j
rep_temp[2] = rep[2] + chg_3 * k
x = self.calculate(raw, rep_temp, 0) / D # 替换后的行列式值 / 原行列式值
y = self.calculate(raw, rep_temp, 1) / D
z = self.calculate(raw, rep_temp, 2) / D
if int(x) == x and int(y) == y and int(z) == z and x >= 0 and y >= 0 and z >= 0:
print("==答案为：")
print(f"规则1按动{int(x)}次")
print(f"规则2按动{int(y)}次")
print(f"规则3按动{int(z)}次")
return True # 注释这一句查看更多答案
return False
@staticmethod
def exist(index: list, num: int) -> int:
return 1 if num in index else 0
# 计算到达180所需的次数
@staticmethod
def count(angle: int, direction: int, rotate: int) -> float:
b = 0
while True:
if angle % 180 == 0 and angle % 360 != 0:
return b
else:
angle = angle - direction * rotate
b += 1
# 行列式计算，输入矩阵matrix如：
# [[1,2,3],
# [1,2,3],
# [1,2,3]]
# 输入系数矩阵如:
# [a, b, c]
# index为替换x/y/z系数索引
@staticmethod
def calculate(matrix_temp: list, replace: list = [], index: int = -1) -> int:
matrix = copy.deepcopy(matrix_temp)
if index != -1:
matrix[0][index], matrix[1][index], matrix[2][index] = replace[0], replace[1], replace[2]
return \
matrix[0][0] * matrix[1][1] * matrix[2][2] + \
matrix[0][1] * matrix[1][2] * matrix[2][0] + \
matrix[0][2] * matrix[1][0] * matrix[2][1] - \
matrix[0][2] * matrix[1][1] * matrix[2][0] - \
matrix[0][1] * matrix[1][0] * matrix[2][2] - \
matrix[0][0] * matrix[1][2] * matrix[2][1]
game = Game()
game.cal()
运行结果
规则2按动一次即可
仓库
https://github.com/Icingworld/CompassCal
发表于 2023-9-22 15:50
|
发表于 2023-9-22 23:44
目的是锻炼代码水平
