题目背景
有一天,小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫,玉蟾宫宫主蓝兔盛情地款待了它们,并赐予它们一片土地。
题目描述
这片土地被分成 $N\times M$ 个格子,每个格子里写着 'R' 或者 'F',R 代表这块土地被赐予了 rainbow,F 代表这块土地被赐予了 freda。
现在 freda 要在这里卖萌。。。它要找一块矩形土地,要求这片土地都标着 'F' 并且面积最大。
但是 rainbow 和 freda 的 OI 水平都弱爆了,找不出这块土地,而蓝兔也想看 freda 卖萌(她显然是不会编程的……),所以它们决定,如果你找到的土地面积为 $S$,它们每人给你 $S$ 两银子。
输入格式
第一行两个整数 $N$,$M$,表示矩形土地有 $N$ 行 $M$ 列。
接下来 $N$ 行,每行 $M$ 个用空格隔开的字符 'F' 或 'R',描述了矩形土地。
输出格式
输出一个整数,表示你能得到多少银子,即 ( 3 $\times$ 最大 'F' 矩形土地面积 ) 的值。
样例 #1
样例输入 #1
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
样例输出 #1
45
提示
对于 $50\%$ 的数据,$1 \leq N, M \leq 200$。
对于 $100\%$ 的数据,$1 \leq N, M \leq 1000$。
题目分析
画个图分析分析
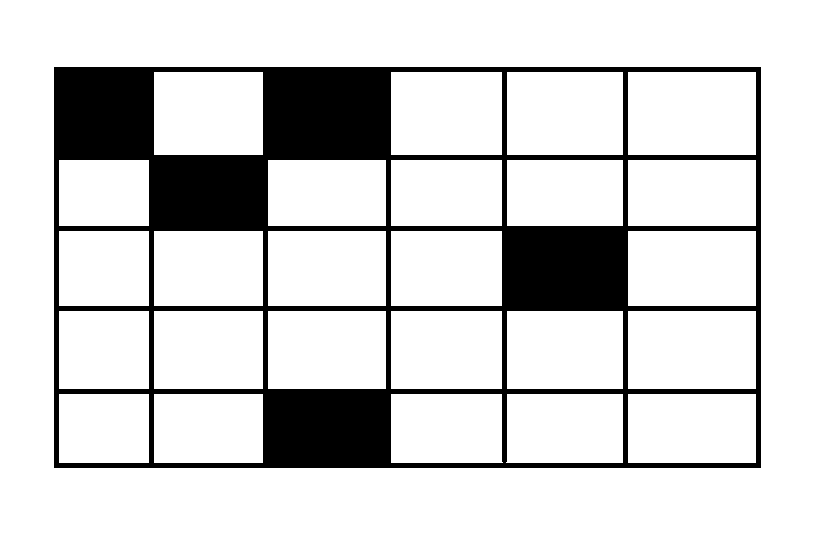
肉眼可见这一块面积最大
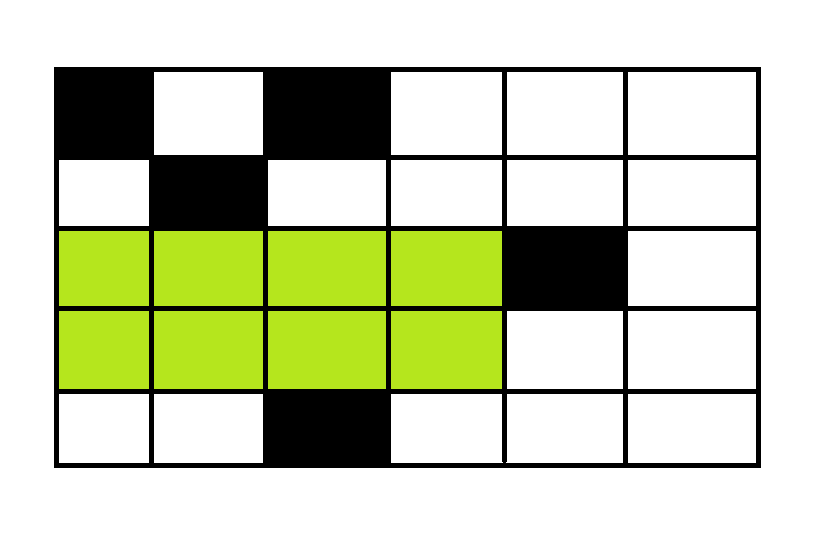
可是我们要如何用编程来求出呢?
以下将 F 设为 “土地” ,将 R 称为 "障碍"
可以想象一下,每一块土地,有一条线,从土地本身一直向上延伸,直到遇到了边界或者障碍,我们把这条线的长度叫 h
我们给每一个土地都计算出它的 h
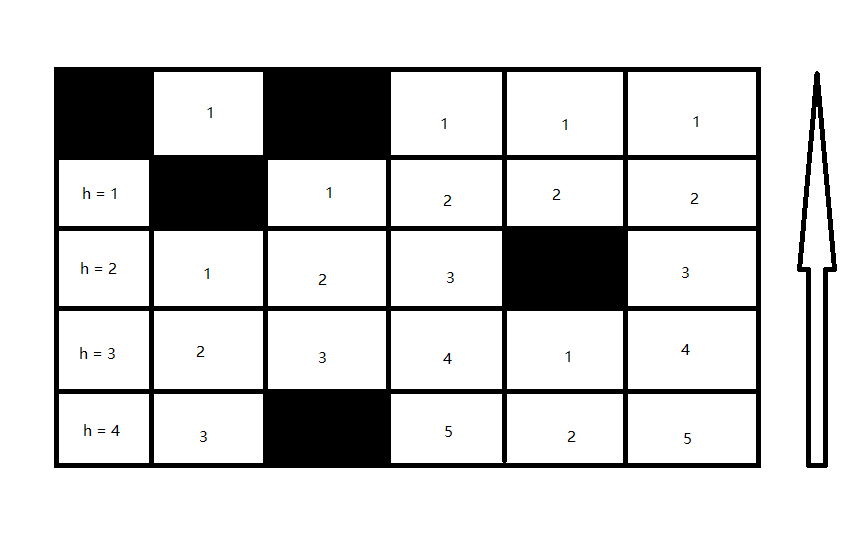
然后,我们要计算每一条线可以往左和右最远可以到达的地方,之后,就可以遍历计算面积并获得最大值了。
那,我们要如何计算每一条线可以往左和右最远可以到达的地方呢?
以下如果不理解,就多看几遍
我们先计算每一个土地可以从自身向左和右可以到达最远的地方,我们叫它 l 和 r 。
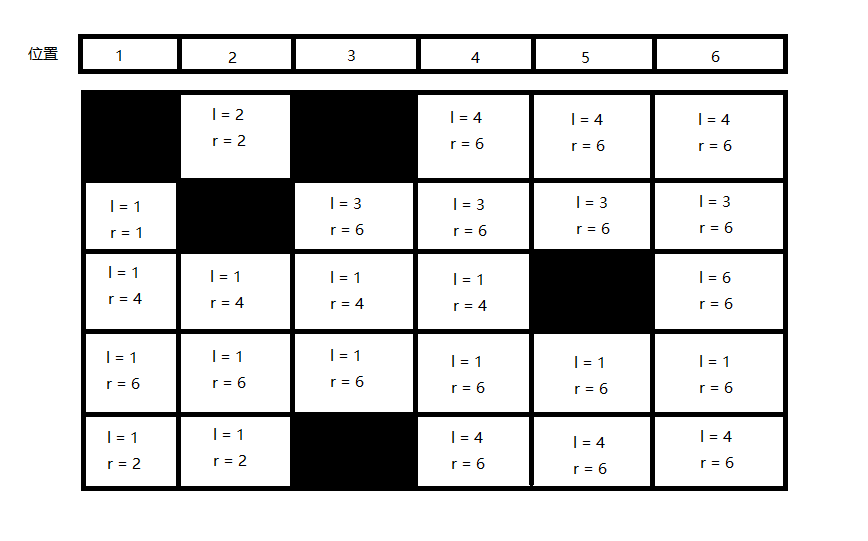
接下来,计算每一条线可以往左和右最远可以到达的地方。当这个土地的上面也是一个土地时,如果上面土地的 r 小于下面的土地,那么下面的土地的 r 更新为上面土地的 r ,如果上面土地的 l 大于下面的土地的 l ,则下面的 l 更新为上面的 l。
可以思考一下,为什么这样做。
更新后的图如下:
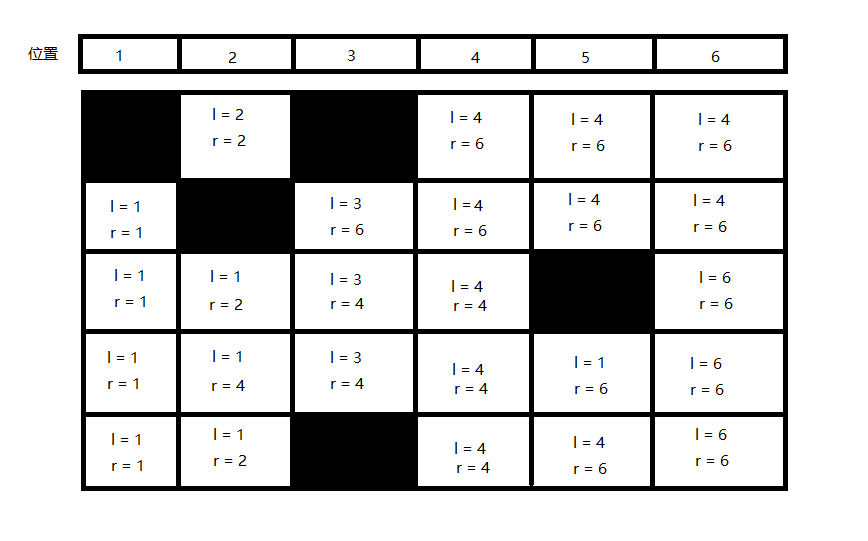
加上前面的关于 h 的图

我们就可以很轻松的获得每条线所可以覆盖的土地面积了
用公式 $(r - l + 1) \times h$ 就可以计算
最后,当全部计算结束,比较大小就可以获得最大的空地面积了
这就是竞赛中常用来解决最大子矩形问题的算法:悬线算法
思路有了,代码开写!
代码开写
根据思路就有四步
第一:读入
过简单,不介绍
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
// 初始化 h
h[i][j] = 1;
}
第二:计算每个土地的 h
// 要计算其他的 h ,如果这个是土地且上面也是土地,则这个土地的 h 等于上面土地的 h 加一
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (a[i][j] == 'F' && i > 1 && a[i - 1][j] == 'F')
h[i][j] = h[i - 1][j] + 1;
第三:计算 r 和 l
// 计算 r 和 l
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 初始化为 j
r[i][j] = j; l[i][j] = j;
}
// 遍历更新
for (int j = 2, k = m - 1; j <= m; j++, k--) {
if (a[i][j] == 'F' && a[i][j - 1] == 'F')
// 对于每一行,如果左边的格子是土地,那么更新为左边格子的 l 加一
l[i][j] = l[i][j - 1];
if (a[i][k] == 'F' && a[i][k + 1] == 'F')
// 对于每一行,如果右边的格子是土地,那么更新为左边格子的 l 加一
r[i][k] = r[i][k + 1];
}
}
for (int i = 2; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (a[i - 1][j] == 'F' && a[i][j] == 'F') {
// 计算每一条线可以往左和右最远可以到达的地方。
// 当这个土地的上面也是一个土地时,如果上面土地的 r 小于下面的土地,那么下面的土地的 r 更新为上面土地的 r
if (r[i - 1][j] < r[i][j]) r[i][j] = r[i - 1][j];
// 如果上面土地的 l 大于下面的土地的 l ,则下面的 l 更新为上面的 l。
if (l[i - 1][j] > l[i][j]) l[i][j] = l[i - 1][j];
}
}
第四:比较最大的面积
// 遍历每一条悬线的面积
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == 'F' && (r[i][j] - l[i][j] + 1) * h[i][j] > ans) {
// 更新最大
ans = (r[i][j] - l[i][j] + 1) * h[i][j];
}
}
}
完整代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1010;
int n, m, ans, h[MAXN][MAXN], l[MAXN][MAXN], r[MAXN][MAXN];
char a[MAXN][MAXN];
int main() {
ans = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
// 初始化 h
h[i][j] = 1;
}
// 要计算其他的 h ,如果这个是土地且上面也是土地,则这个土地的 h 等于上面土地的 h 加一
for (int i = 2; i <= n; i++)
for (int j = 1; j <= m; j++)
if (a[i][j] == 'F' && a[i - 1][j] == 'F')
h[i][j] = h[i - 1][j] + 1;
// 计算 r 和 l
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// 初始化为 j
r[i][j] = j; l[i][j] = j;
}
// 遍历更新
for (int j = 2, k = m - 1; j <= m; j++, k--) {
if (a[i][j] == 'F' && a[i][j - 1] == 'F')
// 对于每一行,如果左边的格子是土地,那么更新为左边格子的 l 加一
l[i][j] = l[i][j - 1];
if (a[i][k] == 'F' && a[i][k + 1] == 'F')
// 对于每一行,如果右边的格子是土地,那么更新为左边格子的 l 加一
r[i][k] = r[i][k + 1];
}
}
for (int i = 2; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (a[i - 1][j] == 'F' && a[i][j] == 'F') {
// 计算每一条线可以往左和右最远可以到达的地方。
// 当这个土地的上面也是一个土地时,如果上面土地的 r 小于下面的土地,那么下面的土地的 r 更新为上面土地的 r
// 如果上面土地的 l 大于下面的土地的 l ,则下面的 l 更新为上面的 l。
if (r[i - 1][j] < r[i][j]) r[i][j] = r[i - 1][j];
if (l[i - 1][j] > l[i][j]) l[i][j] = l[i - 1][j];
}
}
// 遍历每一条悬线的面积
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] == 'F' && (r[i][j] - l[i][j] + 1) * h[i][j] > ans) {
// 更新最大
ans = (r[i][j] - l[i][j] + 1) * h[i][j];
}
}
}
// 输出答案
cout << ans * 3 << endl;
return 0;
}
完结撒花~
 发表于 2024-2-10 21:49
发表于 2024-2-10 21:49