数据结构中的图是什么？
文章内容来自于对王争老师《数据结构与算法之美》栏的学习整理。
图，通常用来表示复杂的关系，一对一、一对多或是多对多。
根据根据图中数据的对应关系可分为：
「无向图」，即 A 关联 B 时，B 同时关联 A。例：微信中当 A 是 B 好友时，B 一定也是 A 的好友（新版本中已支持双向删除好友）。这种关联是双向的。
「有向图」，即 A 关联 B 时，B 未必关联 A。例：微博中粉丝与博主的关系，粉丝关注了博主，但是博主未必关注了每一个粉丝。这种关联性是单向的。
「带权图」，除了表示 A 与 B 是否关联外还表示这种关联度的权重。例如：QQ 空间的好友亲密度。在基本的关联度上附加了其他属性，表示更为复杂的关系。
图中的每一个元素被称为：顶点 。顶点之间表示联系的被称为 边。而顶点所关联的顶点数被称为 度。
在有向图中，顶点 A 所指向的顶点数被称为 出度，而所有指向 A 的顶点数之和被称为顶点 A 的 入度。
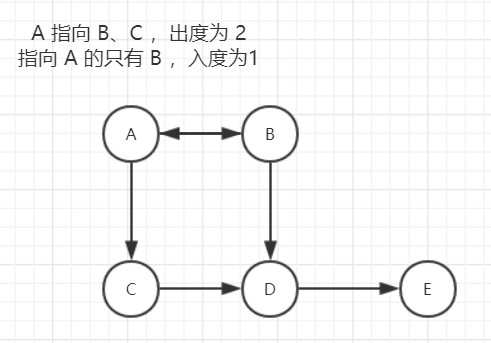
表示方式
邻接矩阵法。即将图中 N 个定点的关系用 N*N 个点组成的表示彼此之间的关联关系
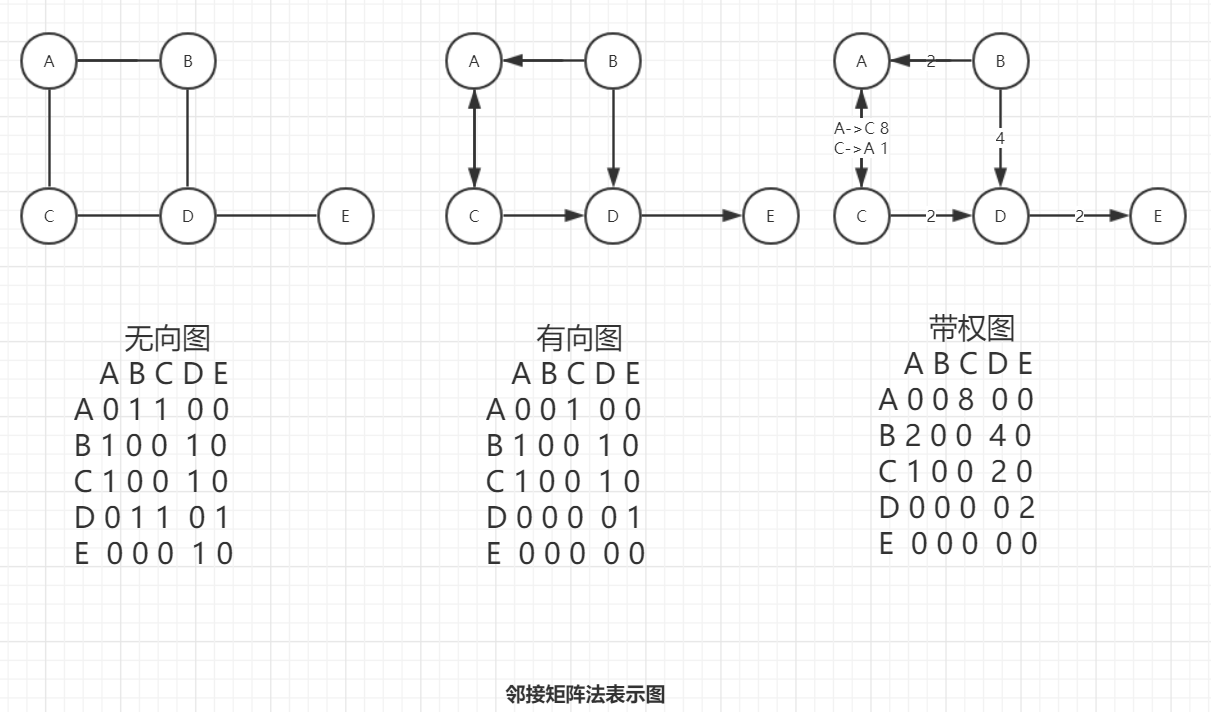
邻接矩阵法。通过 数组 的方式来表示图中各个顶点所对应的关系。
优点：可以通过下标快速获取图中两个顶点所对应的关系。
缺点：在 稀疏图 中会浪费大量的存储空间。（稀疏图：有联点远小于矩阵所能表示的点数，即矩阵中非 0 点数占矩阵的比例）
class ArrayGraph // 数组表示无向表
{
private int[][] graph; // 矩阵表
public ArrayGraph(int n) // N 代表顶点数
{
graph = new int[n][n];
}
public void add(int a,int b) // a,b 代表关联的两个顶点
{
graph[a][b]=1;
graph[b][a]=1;
}
}
邻接表法。通过 链表 存储每一个顶点的 出度 信息。
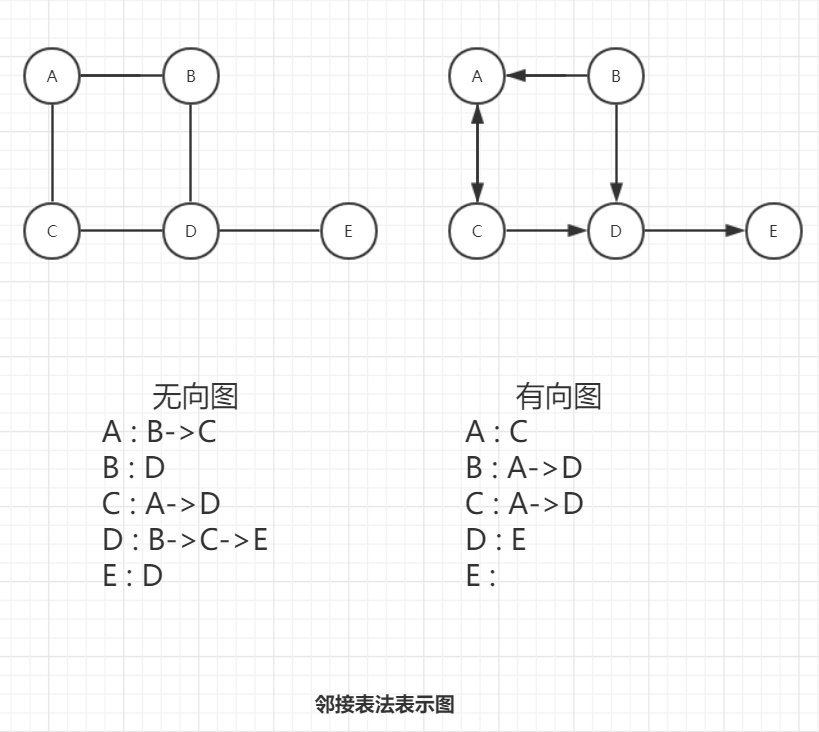
优点，对于 稀疏图 减少了空间消耗。
缺点，对于 浓密图 数据的访问更慢。
class ListGrapg{ // 邻接表法表示图
private LinkedList<Integer>[] graph;
public ListGrapg(int n){ // n 代表图的顶点数
graph = new LinkedList[n];
for(int i=0;i<n;i++)
{
graph[i] = new LinkedList<>();
}
}
public void addLink(int a,int b){ // a,b 代表无向表顶点
graph[a].add(b);
graph[b].add(a);
}
}
图的搜索
广度优先遍历 BFS
广度优先遍历 （Breath-First-Search）是图的搜索中最常用的遍历方式之一，常用于 求最短路径。
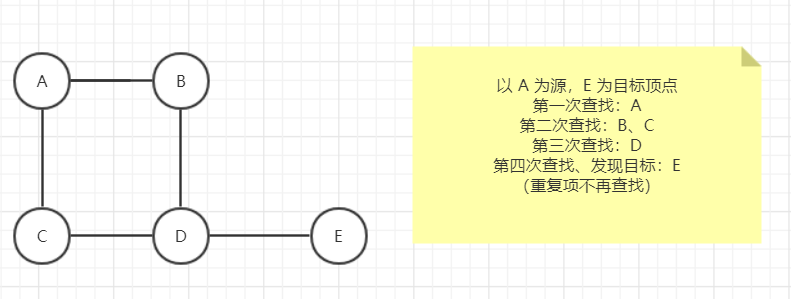
思路：
把图中的任意顶点看做一棵独立的「树」，顶点直接关联的顶点就是树的第二层，以此类推。在查找顶点与另一顶点的最短路劲其实就是从树的根节点依序向下遍历。
public void bfs(int source,int target) // source 为搜索源， target 为搜索目标
{
if(source==target)
return ; // 若查找源即为查找目标则直接返回
boolean[] visted = new boolean[graph.length]; // visted 数组表示当前层是否遍历，若已遍历则设置为 true
visted[source] = true;
Queue<Integer> queue = new LinkedList<>(); // 定义一个数据类型为整数的链表队列，将每次遍历的层加入队列
queue.add(source);
int[] pre = new int[graph.length]; // 定义数组存储遍历的顶点
Arrays.fill(pre, -1); // 将数组 pre 全部初始化为 -1
int dot;
int temp;
int index=0;
while(queue.size()!=0)
{
dot = queue.poll(); // 返回队列首顶点
for(int i=0;i<graph[dot].size();i++)
{
temp = graph[dot].get(i); // temp 为每一次遍历的顶点
if(visted[temp]) // 若该顶点已遍历过则跳过
continue;
pre[index] = temp;
if(temp==target)
{
System.out.print(source+"->");
print(pre, 0, target); // 打印深度遍历的路径
return;
}
index++;
visted[temp]=true;
queue.add(temp);
}
}
}
public void print(int[] pre,int index,int target)
{
if(pre[index]!=target)
{
System.out.print(pre[index]+"->");
print(pre, index+1, target);
}
else{
System.out.print(target);
}
}
深度优先遍历 DFS
深度遍历（Deep-First-Search）。先按照一定顺序向下遍历，若一条路径遍历结束尚未找到，则返回上一分叉点继续遍历下一条路径，知道找到对应目标，结束遍历。
public void dfs(int source,int target)
{
result = false ; // 将查找结果重置回 false
boolean[] visted = new boolean[graph.length]; // 验证该顶点是够已被访问
int[] pre = new int[graph.length];
Arrays.fill(pre, -1);
recurDfs(source,target,visted,pre,0);
System.out.print(source+"->");
print(pre, 0, target);
}
public void recurDfs(int source,int target,boolean[] visted,int[] pre,int index) // 回溯法实现深度遍历
{
if(source==target)
{
pre[index]=source;
return ; // 找到对应目标返回
}
visted[source]=true;
for(int i=0;i<graph[source].size();i++)
{
int temp = graph[source].get(i);
if(visted[temp])
continue;
pre[index]=temp;
index++;
recurDfs(temp, target, visted, pre, index);
}
}
总结，深度遍历像俗话说的「一条道走到黑」，只要路还能往下走就会一直向下遍历，直到撞了南墙才会回头。（文章中出现错误，可以直接在评论中指出）
发表于 2019-4-15 15:18
|
发表于 2019-4-16 09:16
这是在哪copy的吗？ - -|| 图咋没了... 大标题广搜的缩写是BFS..... 